beräkning av sned asymptot

Uppgiften jag har är att beräkna alla asymptoter för funktionen f(x)= $\frac{x^{2} a r c \tan (x)}{x - 1}$

Jag har problem med de sneda asymptoterna. Jag har funnit k-värdet som $\frac{π}{2}$ men kan inte för mitt liv få till m-värdet. Jag vet att man ska beräkna $\lim_{x \to \infty} f (x) - k x$ men kommer inte längre än att sätta differensen på samma bråkstreck. Jag har en aning att tanken med uppgiften är att man ska använda L'hopital, men hur?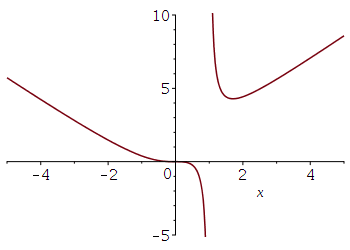

Du får väl $\frac{x (\arctan x - \frac{π}{2}) + π / 2}{1 + 1 / x}$ ?

Visa med L’hospital att $x (\arctan x - π / 2)$ går mot -1 då x går mot oändlighet.

$\lim_{x \to \infty} \frac{x^{2} (a r c \tan x - π / 2) - (π / 2) x}{x - 1}$

Jag tänkte att man ska dela upp bråket i två delar, där den senare termen går mot $\frac{π}{2}$ när x går mot oändligheten

Men den första delen får jag inte till L'Hopital med, för $x^{2} (a r c \tan x - π / 2) = \infty \times 0$ , kan jag få hela den första termen i formen $\frac{0}{0}$ så att jag kan applicera L'H?

Du har den första delen som

$\frac{x^{2} (\arctan x - π / 2)}{x - 1} = \frac{x (\arctan x - π / 2)}{1 - 1 / x}$ .

Nämnaren går mot 1 då x går mot oändlighet.

Du kan visa med L’hospital att täljaren går mot -1 då x går mot oändlighet.

$x (\arctan x - π / 2) = \frac{\arctan x - π / 2}{1 / x}$ , fallet 0/0.

Jag löste den nu, tack!

Svara

Visa senaste svar