Beräkning av volym med avvikelse
Det som jag vet:
r= 2,5cm
h=15cm
vill räkna ut volymen med avvikelse och formen är en cylinder. Gör jag rätt?

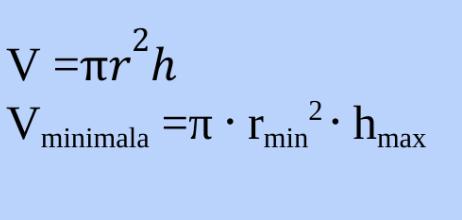
Gör jag rätt? Ska man ta minimala radien och maximala höjden eller ska både vara min för vi förösker hitta den minsta volymen?
Jag undrar också om linjal har mätnggranheten 0.05cm? Tack i efterhand.
Hur lyder frågan, mer specifikt? Har du fått någon osäkerhet i höjdmåttet, eller vet vi säkert att ?
Om du vill hitta den maximala möjliga avvikelsen, behöver du beräkna den största respektive minsta möjliga volymen, vilket du får genom att räkna med de maximala måtten på höjd och radie, respektive de minimala måtten för höjd och radie. :)
Smutstvätt skrev:Hur lyder frågan, mer specifikt? Har du fått någon osäkerhet i höjdmåttet, eller vet vi säkert att ?
Om du vill hitta den maximala möjliga avvikelsen, behöver du beräkna den största respektive minsta möjliga volymen, vilket du får genom att räkna med de maximala måtten på höjd och radie, respektive de minimala måtten för höjd och radie. :)
Jag har mät den med vanlig linjal
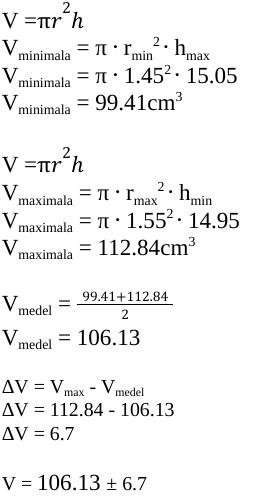 Detta har jag kommit fram men känns inte rimligt eller?
Detta har jag kommit fram men känns inte rimligt eller?
Omar2022 skrev:Det som jag vet:
r= 2,5cm
h=15cm
vill räkna ut volymen
Volymen är
Eller bättre
Pieter Kuiper skrev:Omar2022 skrev:Det som jag vet:
r= 2,5cm
h=15cm
vill räkna ut volymen
Volymen är
Eller bättre
Ja men jag vill räkna med avvikelse
Omar2022 skrev:Pieter Kuiper skrev:Omar2022 skrev:Det som jag vet:
r= 2,5cm
h=15cm
vill räkna ut volymen
Volymen är
Eller bättreJa men jag vill räkna med avvikelse
Gör det då, med värden som i uppgiften.
Vmax = pi.rmax2hmax
Vmin = pi.rmin2hmin
Smaragdalena skrev:Vmax = pi.rmax2hmax
Vmin = pi.rmin2hmin
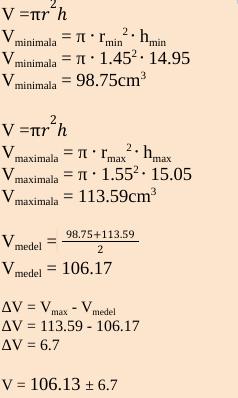
om r = 1.5 cm
Ska jag göra så?
Omar2022 skrev:Det som jag vet:
r= 2,5cm
Vet du säkert?
Pieter Kuiper skrev:Omar2022 skrev:Det som jag vet:
r= 2,5cm
Vet du säkert?
Mätte med linjal, därför vill jag ha ett resultat med felmarginal
Omar2022 skrev:
Mätte med linjal, därför vill jag ha ett resultat med felmarginal
Då borde 1,5 cm ligga utanför felmarginalen.
jag har tidigare skrivit fel mätningen visade 1.5 cm och tänkte linjal har avvikelse 0.05 cm därför:
1.55 maximala
1.45 minimala




