Berg- och dalbana - resonemang
Hej!
Jag skulle i denna uppgift bestämma vilken graf som visar hur vagnens fart ändrades då avståndet från mittvagnen till toppen ökade. Jag tänkte bara rimligt att när vagnen är högst upp har den som lägst fart, därav kan man utesluta D och f som är negativa funktioner kan man säga. Ju längre vagnen åker nedåt för banan desto snabbare går den, därav är det inte A. Då står det mellan B, C och E. Sedan fortsätter ju farten inte att öka exponentiellt som i B, för vi har ju krafter som påverkar vagnen och gör att den inte konstant kan accelerera då den inte har en motor. Då är C rätt. Men denna förklaring är inte ett dugg matematisk, så jag undrar vad jag hade kunnat förbättra för att plocka alla poäng i denna fråga. Hur kan jag motivera att de avtagande graferna tex inte kan stämma?

Jag hade utgått från formeln
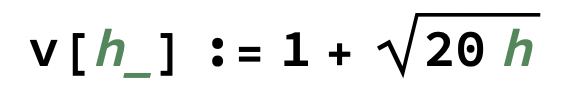
v[0] = 1 vilket eliminerar D och F (vi får här anta att de är ritade med samma skala, vilket är tydlig för ABCE som alla har samma y-värde för h=0.
Den "aktiva" delen i v[h] är sqrt(h) och den har alltid formen av C. sqrt(20) är bara en skalfaktor.
Just det. Tänkte inte så noga på själva formeln. Redan där, eftersom att det är en rot i formeln så vet man ju att grafen kommer se ut som i C eftersom att det är så grafer till funktioner som den är formade. De övriga graferna hör till andra typer av funktioner. Tex B som är en andragradare eller A som är en förstagradsfunktion, även F är det men den är nedåtgående.
Jag kan dock inte motivera varför grafen till en funktion med sqrt har just den formen, förutom att olika värden på h ger punkterna i den grafen. Men det är inte ett "färdigt" argument skulle jag säga.
Jag tror man får utgå från en viss grundläggande grafkunskap i denna uppgift men man kan t.ex. säg att
-- y=1+sqrt(20h) har inversen h=1/20(y-1)^2 och det finns bara en graf (C) som beskriver en sådan parabel för inversen.
Hade vi inte haft vetskap om funktionen hade man säkert kunnat motivera många av de andra graferna genom div. fysikaliska och mekaniska argument.
det finns bara en graf (C) som beskriver en sådan parabel för inversen.
Vad menas med detta?
Och jag tycket det är svårt att veta vad man ska kunna om grafer som just ingår i den grundläggande grafkunskapen. Jag har tex aldrig stött på det om inversa funktioner som ger en viss graf. Googlade en snabbis om inversa funktioner, det verkar som att det ingår i matte 4 om inte jag har helt fel. Men hur mycket tror du att man egentligen behöver kunna om grafer och funktioner utöver vilken typ av funktion som ger ett visst utseende på grafen och hur man kan göra småändringar i funktionen som kan ändra grafens utseende på olika sätt?
KlmJan skrev:det finns bara en graf (C) som beskriver en sådan parabel för inversen.
Vad menas med detta?
Och jag tycket det är svårt att veta vad man ska kunna om grafer som just ingår i den grundläggande grafkunskapen. Jag har tex aldrig stött på det om inversa funktioner som ger en viss graf. Googlade en snabbis om inversa funktioner, det verkar som att det ingår i matte 4 om inte jag har helt fel. Men hur mycket tror du att man egentligen behöver kunna om grafer och funktioner utöver vilken typ av funktion som ger ett visst utseende på grafen och hur man kan göra småändringar i funktionen som kan ändra grafens utseende på olika sätt?
Jag tycker det räcker med "små kunskaper". Man skall veta vad:
-- "+C" där C är en konstant gör för grafen
-- vad C f(x) gör för grafen (skalning) (men även en spegling i x-axeln för vissa C)
-- vad f(Cx) gör för grafen (en 'krökning' eller 'flackning', för trig. funktioner innebär detta förändrad vinkelhastighet, spegling, etc.)
Då klarar man sig fint.
Jag tror dock inte du behöver gräva ner dig alltför mycket i detaljer för ett prov. Man skall ha en koll på läget, inte skriva en avhandling.
Lite 'trivia'. Kort efter kometen hade utrotat alla djuren, före grafritarnas tid, hade man kurvmallar. De fanns endast i en skepnad för varje "känd" funktion, t.ex. y=1/x, y=1/x^2, y=x^2. Med dessa kanske 5-6 grafer skulle man sedan rita en mängd andra funktioner, t.ex. y=1+2/(3-x) etc. Man hade bara en mall för varje typ av funktion och det gällde att flytta runt denna på pappert och välja rätt skalor på axlarna. Det var en bra övning. Allt detta försvann med räknare och jag tror idag att de flesta elever har en aning sämre "känsla" för grafer än förr. Visst, man kan leka med lite parametrar i GGB och se vad som händer på skärmen, men inget går upp att bli "smutsig om händerna".
Notera att y=x^2 har inversen x=sqrt(y) och man fick alltså använda parabel-grafen till att rita rot-kurvan. Detta eviga tjat och ritande gjorde att man alltid, som ren reflex, sammankopplade funktioner med deras invers. Allt det går förlorat med grafritare. Sedan finns det MÅNGA fördelar med grafritare. Vi skall inte bromsa utvecklingen.


