Besgäm tröghetstensorns samliga komponenter
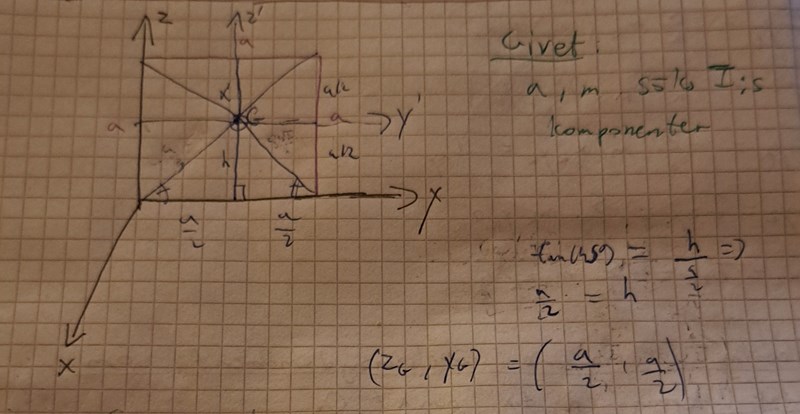
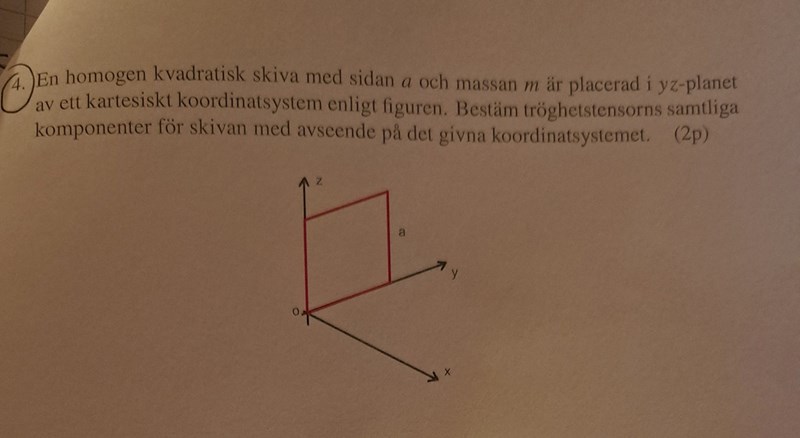
Såhär långt har jag kommit och vill använda parallellförflyttningssatsen för tröghetsprodukter men är fast på hur jag ska göra det
Börja med att bestämma tröghetstensorn (matrisen) IG relativt ett koordinatsystem med origo i masscentrum G och axlar parallella med axlarna i figuren.
Om IO är tröghetsmatrisen i O så gäller följande samband.
IO = IG +
PATENTERAMERA skrev:Börja med att bestämma tröghetstensorn (matrisen) IG relativt ett koordinatsystem med origo i masscentrum G och axlar parallella med axlarna i figuren.
Om IO är tröghetsmatrisen i O så gäller följande samband.
IO = IG +
Vad är detta för formel? Jag känner inte igen detta. Om du använder parallellförflyttningssatsen för tröghetsprodukter vill jag minnas att det är I_O=m*x_gy_g+Ix'y'
Nja, tänk att du börjar med att beräkna IG ; sedan lägger du till den tröghetsmatris som (enligt koordinatsystemet i O) du får om du placerar en partikel med massa m i plattans masscentrum.
AI-utläggning.

PATENTERAMERA skrev:Nja, tänk att du börjar med att beräkna IG ; sedan lägger du till den tröghetsmatris som (enligt koordinatsystemet i O) du får om du placerar en partikel med massa m i plattans masscentrum.
AI-utläggning.
Det låter som en krånglig metod att minnas inför en tenta. Finns det annat sätt man kan ta fram komponenterna tex mha parallellförflyttningssatsen för tröghetsprodukter eller vanliga matematisk integrering? Det här sättet har inte introducerats i kursen heller
Det är ju det som formeln sammanfattar.
Tex
DOxy = DGxy + mxGyG.
PATENTERAMERA skrev:Det är ju det som formeln sammanfattar.
Tex
DOxy = DGxy + mxGyG.
jag vet inte vad detta är för formeln men om det är för tröghetsprodukter så är det inte användarbart här eftersom det var krånglig matris man ska komma ihåg och skapa. . Det är därför jag frågar om en annan metod vid en pressad tentasituation, sen har vi aldrig jobbat med den här typen av metoden du har gjort med AI osv.
Det är formeln för tröghetsprodukter.
Vilken metod finns i boken/föreläsningar? Visa den och hur du tänkt att använda den.
PATENTERAMERA skrev:Vilken metod finns i boken/föreläsningar? Visa den och hur du tänkt att använda den.
jag har ingen bok justnu att visa. Men jag tänkte integrera istället för jag kommer tyvärr inte minnas den här krångliga sättet med tröghetsprodukter som AI gör och det såg väldigt arbetssamt ut, det lilla jag minnas av tröghetsprodukter är Ixy =Ig+Ix'y'. Såhär gjorde facit
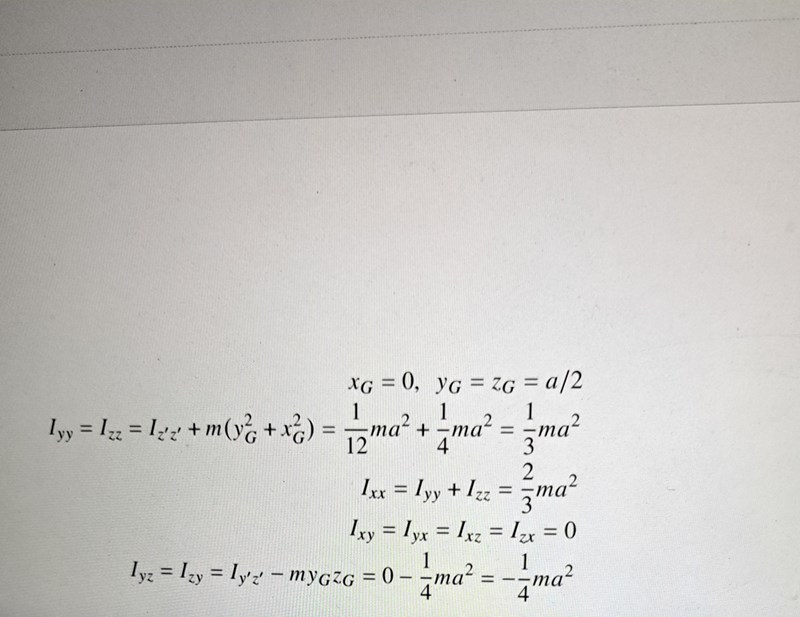
Jag tror att de har använt parallellförflyttningssatsen för tröghetsprodukter. Jag skulle dock vilja förstå hur de fick fram alla komponenter.
1) varför är x_G=0 och z_g=y_G=a/2?
2) De har skrivit Iyy=Izz=Iz'z'+m(x_G^2+y_G^2). Jag förstår inte var denna formel kommer ifrån och vad Izz och Izz(prim) motsvarar och hur de hittade den ?
3) sen skriver de Ixx=Izz+Iyy=2/3ma^2. Hur får de detta?
4) varför är Ixz=Ixy=Izx=Iyx=0?
5) varför är Iy'z'=0?
Du behöver inte använda parallellaxelsatsen. Du kan integrera rakt av.
, där integrationen sker över kvadraten i yz-planet.
destiny99 skrev:PATENTERAMERA skrev:Vilken metod finns i boken/föreläsningar? Visa den och hur du tänkt att använda den.
jag har ingen bok justnu att visa. Men jag tänkte integrera istället för jag kommer tyvärr inte minnas den här krångliga sättet med tröghetsprodukter som AI gör och det såg väldigt arbetssamt ut, det lilla jag minnas av tröghetsprodukter är Ixy =Ig+Ix'y'. Såhär gjorde facit
Men det är ju precis vad matrisformeln säger, fast utskrivet komponentvis.
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:Vilken metod finns i boken/föreläsningar? Visa den och hur du tänkt att använda den.
jag har ingen bok justnu att visa. Men jag tänkte integrera istället för jag kommer tyvärr inte minnas den här krångliga sättet med tröghetsprodukter som AI gör och det såg väldigt arbetssamt ut, det lilla jag minnas av tröghetsprodukter är Ixy =Ig+Ix'y'. Såhär gjorde facit
Men det är ju precis vad matrisformeln säger, fast utskrivet komponentvis.
Se #11
PATENTERAMERA skrev:Du behöver inte använda parallellaxelsatsen. Du kan integrera rakt av.
, där integrationen sker över kvadraten i yz-planet.
Jag vet inte hur man gör på det sättet och vad du försöker integrera. Vad är -m/a^2 och var kommer den ifrån?
Normalt så definieras tröghetsprodukten Dyz som
.
Men eftersom du har ett plant föremål K (kvadrat) så får vi definiera det som
, där är ytdensiteten.
Sedan gäller det att Iyz = -Dyz.
destiny99 skrev:Jag tror att de har använt parallellförflyttningssatsen för tröghetsprodukter. Jag skulle dock vilja förstå hur de fick fram alla komponenter.
1) varför är x_G=0 och z_g=y_G=a/2?
2) De har skrivit Iyy=Izz=Iz'z'+m(x_G^2+y_G^2). Jag förstår inte var denna formel kommer ifrån och vad Izz och Izz(prim) motsvarar och hur de hittade den ?
3) sen skriver de Ixx=Izz+Iyy=2/3ma^2. Hur får de detta?
4) varför är Ixz=Ixy=Izx=Iyx=0?
5) varför är Iy'z'=0?
1) Detta är masscentrums koordinater. Ligger mitt i skivan.
2) Oprimmat är tröghetsmomentet kring O. Primmat är kring G. Izz = Iyy pga symmetri.
3) Det beror på att vi har ett platt föremål. Då är tröghetsmomentet kring en axel vinkelrät mot föremålet lika med summan av tröghetsmomenten kring de andra två axlarna. Här är x-axeln vinkelrät mot skivan.
4) Skivan ligger i yz-planet. x = 0 överallt i skivan.
5) Symmetri igen.
Du kan enkelt integrera fram svaret på 5).
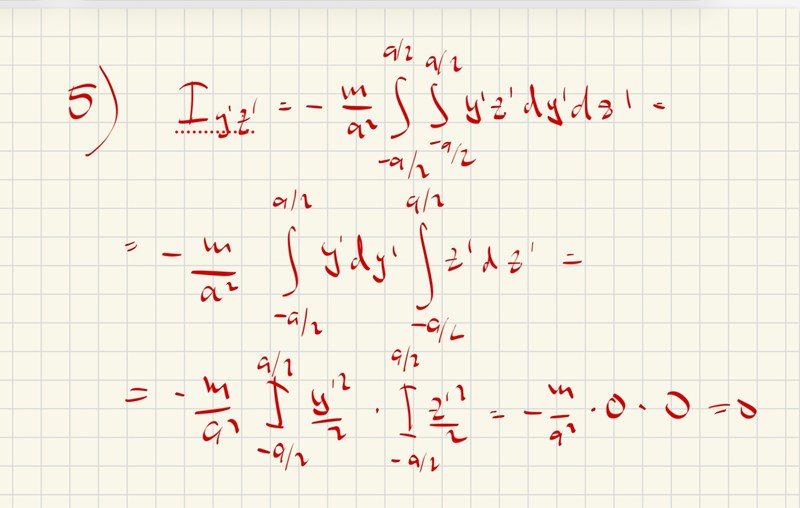
PATENTERAMERA skrev:Du kan enkelt integrera fram svaret på 5).
Chatgpt gjorde på följande vis med integrering. Då är dm=m/a^2 dzdy eller hur?


Ja, helt rätt om dm.


