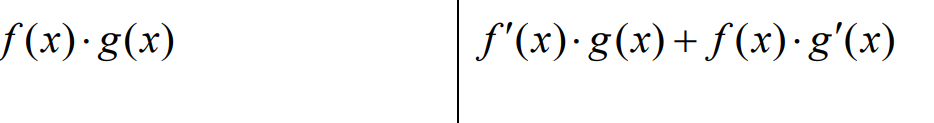Bestäm 2:a derivatan av h

h'(x) är rätt. Vad blir h''(x)?

Laguna skrev:

h'(x) är rätt. Vad blir h''(x)?

Då kan jag väl derivera igen för att få fram 2:a derivatan.

Arup skrev:

Laguna skrev:

h'(x) är rätt. Vad blir h''(x)?

Då kan jag väl derivera igen för att få fram 2:a derivatan.

Ja

så blir det då:

$$\begin{gathered} D(h\text{'}(x\left)\right)=D(2\times f(x)\times f\text{'}(x\left)\right) \\ h\text{'}\text{'}\left(x\right)=2\times f\text{'}\left(x\right)\times f\text{'}\text{'}\left(x\right) ? \end{gathered}$$

Nej, använd produktregeln.

Jag tycker det lite svårt att derivera med produkt regeln om vi inte har funktion på formen $y=kx+m$eller $y=a{x}^2+bx+c$

Jag tänker spontantg på 

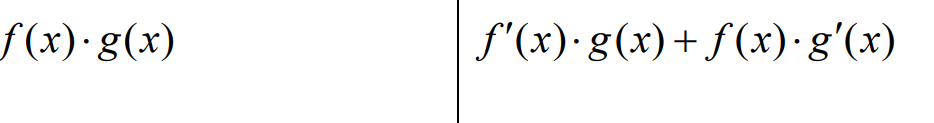
Skulle du kunna visa ?

Arup skrev:

Jag tycker det lite svårt att derivera med produkt regeln om vi inte har funktion på formen $y=kx+m$eller $y=a{x}^2+bx+c$

Jag tänker spontantg på 

Skulle du kunna visa ?

Exakt den reglen skall du använda på

2f * f'

Du får

D(2f) * f' + 2f * D(f')

Kan du utveckla detta?

Trinity2 skrev:

Nej, använd produktregeln.

Ska det bli så här ?

f(0)*f''(0) får du till 3*2, men f(0) är inte 3.

Ok, men allt annat när det kommer till uträkning var väl rätt ?

En rad börjar

h''(x) = 2*f'(x)*f'(x) ...

och på nästa rad står det

h''(x) = f'(x)*(2*1) ...

Hur gick det till?

Jag brlt ut ett f'(x)

Tillägg: 29 dec 2025 11:13

bröt*

Ser du att det inte stämmer?

varför skulle du inte funka med att bryta ut ett $f\text{'}\left(x\right) ?$

Arup skrev:

varför skulle du inte funka med att bryta ut ett $f\text{'}\left(x\right) ?$

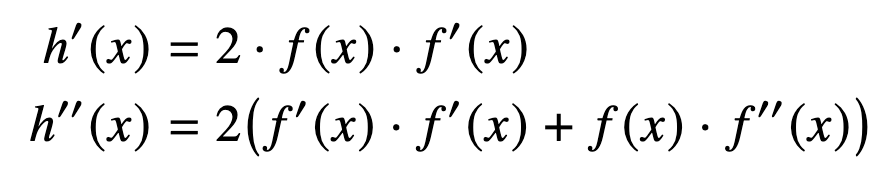
Sätt nu in x=0 och använd informationen från uppgiften.

Arup skrev:

varför skulle du inte funka med att bryta ut ett $f\text{'}\left(x\right) ?$

Om du bryter ut rätt, ja.

Varför skulle f'(x)*f'(x) vara lika med f'(x)?