Bestäm a & b så att ekvationssystemet har oändligt många lösningar.
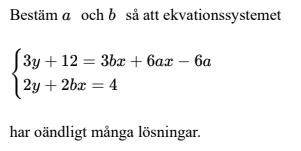 Har ett prov imorgon och har klarat alla tidigare uppgifter på övningsprovet, förutom denna.
Har ett prov imorgon och har klarat alla tidigare uppgifter på övningsprovet, förutom denna.
Jag förstod tillräckligt för att få C poängen på uppgiften men förstår inte hur man löser uppgiften.
Jag har löst ut y till båda (det ger C poäng) men har fastnat där.
Ser ut såhär:
y=bx+2ax-2a-4
y=2-bx
Jag förstår inte hur jag ska fortsätta för att få svaren till a & b så att båda ekvationerna får samma svar (blir oändliga).
Välkommen till Pluggakuten! Utmärkt början! Först behöver vi se till att linjerna har samma lutning. Detta kan vi göra genom att lösa ut x, så att det är lätt att läsa av värdena för x:
Dessa två konstanter måste vara lika, och det ger oss ekvationen .
Nu går det att göra samma sak, men med konstanttermerna. De måste vara lika. Vilken ekvation kan du ställa upp som beskriver detta? :)
Hej och välkommen till Pluggakuten!
Utmärkt början!
Du har råkat skriva fel på första ekvationen, det ska vara y = bx + 2ax - 2a - 4
Tips:
Faktorisera ut x ur högerledets första två termer i ekvation 1.
Byt plats på de båda termerna i högerledet i ekvation 2.
Du kommer då att ha två linjära ekvationer enligt mallen
För att dessa båda ekvationer ska ha oändligt många lösningar måste de vara identiska, dvs det måste gälla att och att .
Kommer du vidare då?
Tack så mycket! Jag tror jag förstår, jag rätta även till felet jag skrivit från början.
Nu har jag :
y = x(b+2a)-2a-4
y = 2-bx
Som Smutstvätt berätta så blir b+2a=-b eftersom att de är k värdet och för att de ska vara oändliga så måste de vara lika, korrekt?
Utifrån det kunde jag skriva (vet ej om det är smidigt sätt) :
y = -bx-2a-4
y = -bx+2
Eftersom att båda är lika med y värdet så kan jag skriva :
-bx-2a-4 = -bx+2
Från detta kan jag addera bx på båda sidor:
-2a-4=2
Med detta kan jag få svaret a=-3
Nu är istället nästa fråga, vart är det smidigast att placera in a för att få svaret till b?
Du har ju tidigare kommit fram till att b+2a=-b. Stoppa in att a=-3 och lös ut b.
Visa spoiler
Jag skulle ha löst ut a ur b+2a=-b och fått fram att a=-b redan där, men ditt sätt funkar lika bra.
Smaragdalena skrev:Du har ju tidigare kommit fram till att b+2a=-b. Stoppa in att a=-3 och lös ut b.
Visa spoiler
Jag skulle ha löst ut a ur b+2a=-b och fått fram att a=-b redan där, men ditt sätt funkar lika bra.
Justee haha, tack så mycket.
b+2a=-b
b+2(-3)=-b
b-6=-b
2b=6
b=3
Så svaret blir
Tack allihopa!




