Bestäm a så rotationsvolym blir maximal

Först utav allt ska vi hitta integrand gränserna för rotationen. Vi vet att den övre gränsen är 1 och för att hitta den undregränsen tar vi och hittar nollpunkterna för funktionen. Så 0=$\sqrt{ax-a^2}\left\{0<a<1\right\}$vi får då att a=x är den enda lösningen för a får inte vara noll, så den undre integrand gränsen är a. Vi får att y²=ax-a² och nu integrar vi detta på det vanliga sättet för en rotationskropp runt x axeln då a är en konstant med integrandgränserna a som undre och 1 som övre. Då kommer vi får pi((a/2-a²)-(a³/2-a³) detta kommer nu vara en funktion för arean som beror på vad konstanten a är, så vi kan förenkla och sedan derivera den för att hitta extrempunkter och sedan ta andra derivatan med dem värdena för extrempunkterna för att bekräfta en maxpunkt. 

Okej. Hur vet man att man vill hitta nollpunkten för den undre gränsen?

Kunde förenkla uttrycket till a/2 -a^2 + a^3/2

Och sedan derivatan borde vara 1/2 - 2a +(3a^2)/2. Fast det går inte ihop sen när jag tar på formel så det är väl fel 

Dkcre skrev:

Okej. Hur vet man att man vill hitta nollpunkten för den undre gränsen?

Kunde förenkla uttrycket till a/2 -a^2 + a^3/2

Och sedan derivatan borde vara 1/2 - 2a +(3a^2)/2. Fast det går inte ihop sen när jag tar på formel så det är väl fel 

Du verkar ha gjort rätt;

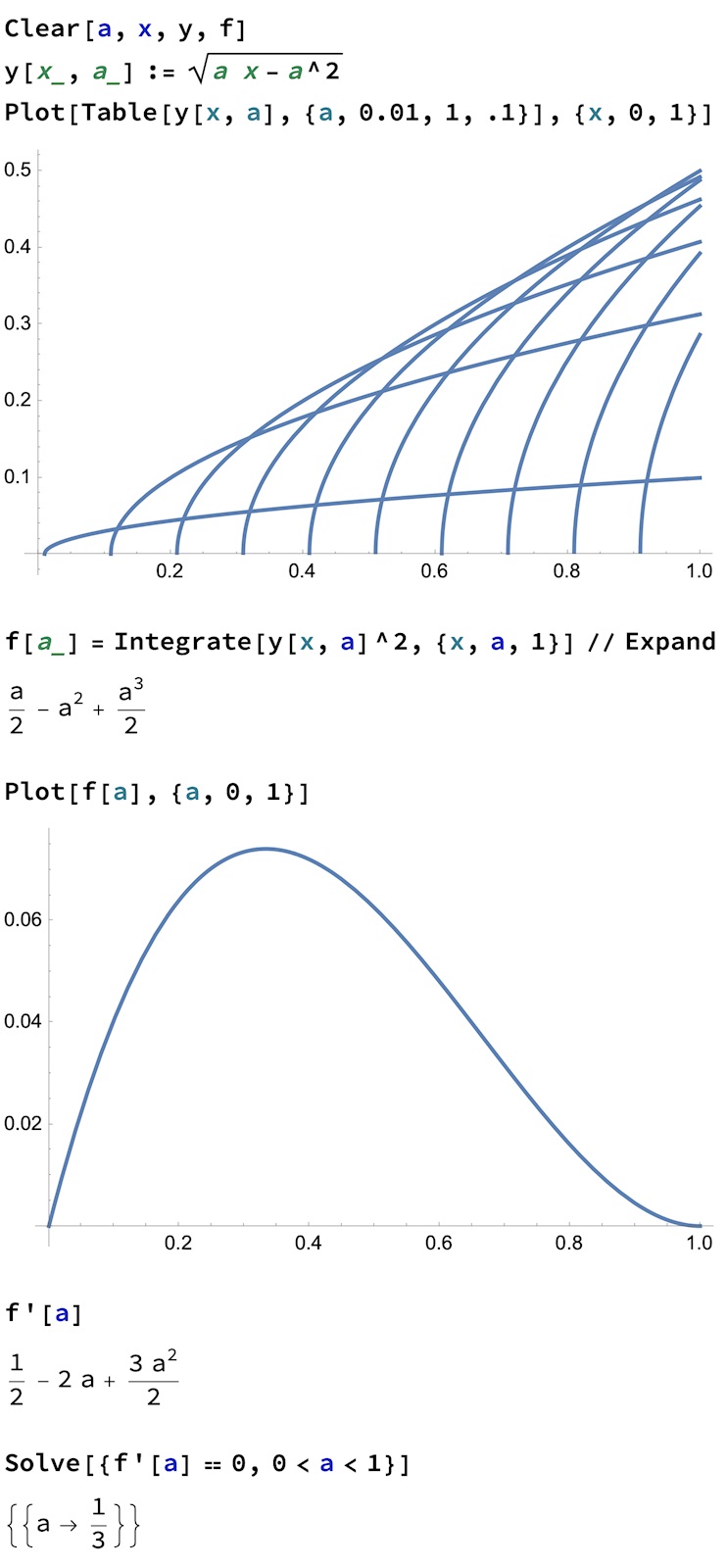
Har du hittat då derivatan är noll och checkat om det är en max eller mini punkt? testade själv och fick att volymen blev som mest då a=1/3.

Det är inte så att derivatan för utrycket blir det som är a för maximumet utan att du måste se a som en variabel i den funktionen för volymen och då hitta med hjälp av derivata det a som gör volymen störst.

Det kan ha varit jag som var lite otydlig med vad a var i den volym funktionen och därav vad derivatan skulle betyda. 

Du var inte otydlig! Jag tycker bara att det här är väldigt, väldigt svårt.

Men löste det.. ja, typ.

Tack för hjälpen 👍

Dkcre skrev:

Okej. Hur vet man att man vill hitta nollpunkten för den undre gränsen?

Kunde förenkla uttrycket till a/2 -a^2 + a^3/2

Och sedan derivatan borde vara 1/2 - 2a +(3a^2)/2. Fast det går inte ihop sen när jag tar på formel så det är väl fel 

Om den undre integrandgränsen inte skulle vara vid nollpunkten skulle vi antagligen ta en punkt då funktionen icke är definerad eller negativ och då skulle vi få en mindre volym för volymen som körs under x axeln blir negativ eller en icke-real, annars om vi tar en punkt som är icke en nollpunkten fast funktionen har ett positivt värde så missar den volymen så är där så om vi vill maximera volymen måste vi ta nollpunkten om inget annat ges.