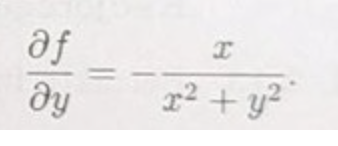Bestäm alla funktioner f(x,y) sådana att
Hej! Jag fattar inte uppgift b på denna jag prövade variabelsubstitution, först
x2+y2=u samt du=ydx (m.a.p x) och x2+y2=v samt dv=xdy (m.a.p)
prövade detta och fick typ -ln u + ln u + C = C (vilket var fel, fine det make:ar sense för deriverar vi en konstant m.a.p så så kommer vi inte få någon av de (däremot så får vi ju faktiskt två olika konstanter C(x) och K(y)) men whatever.
Sen prövade jag denna substitutionen:
x=cos
y=sinθ
dx,dy = dθ
och jag fick typ sinθ - cosθ + C=f(x,y) , vilket också var fel (även om vi löser ut vad θ är från ovan)
Okej då tänkte jag att det kanske är skrivet på någon form jag känner till (en känd derivata eller något) men idk... behöver hjälp tack!
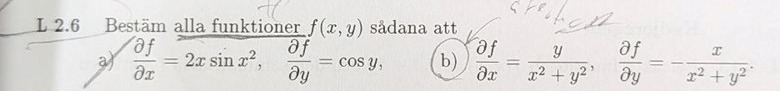
"L" betyder Löst och finns längre bak i boken.
Trinity2 skrev:"L" betyder Löst och finns längre bak i boken.
jaha, tackar. Vad betyder "T"?
edit: ahhhh, Tips... coolt!
Edit 2: Nej vänta de visade bara för deluppgift a) men inte b)... vet fortfarande inte hur man gör
Vad säger tipset? Kan visad lösning används för b)
Finns inget :(
Jag hade fokuserat på
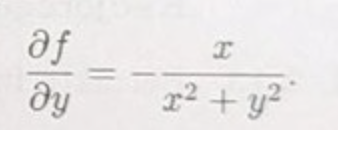
Bryt ut x^2 ur nämnare och förenkla så ser du klarare vad du söker.
Trinity2 skrev:Jag hade fokuserat på
Bryt ut x^2 ur nämnare och förenkla så ser du klarare vad du söker.
Ahhh, så får man arctan derivatan... tack så mycket... det blidde rätt