Bestäm alla k s.a. 7834^k kong. med 6850 (mod 8613): förstår ej facits metod

Hej!

Jag förstår inte riktigt varför facit anger att x ska vara kongruent med mod 9, mod 10 och mod 14, i nedanstående lösning, och hur man kommer fram till vad alla lösningar blir i första laget.

Uppgift och facit:

"vår isomorfi" är definierat tidigare i häftet

För enkelhetens skull kan vi väl fokusera på uppgift b).

Här förstår jag varför man kan använda bijektionen på det sättet att $f(x)^k=f(x^k)$

alltså

$f(7834)^k=(4^k, 2^k, 4^k)$. Sen är $f(6850)=(1,8,6)$.

Så vi söker väl, som jag tolkat det, alla tal som uppfyller:

$4^k \equiv_{27} 1$

$2^k \equiv_{11} 8$

$4^k \equiv_{29} 6$

(eftersom koordinaterna motsvarar räkning i Z27, Z11 och Z29 respektive).

Och sen beräkngar facit då med prövning $4^k, 2^k$ för några olika $k$ och i de olika $\mathbb Z_m$ som uppgiften täcker.

Men varför får vi 

och hur leder det till

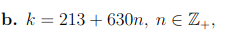
Har det någonting med ringisomorfin att göra? Men har verkligen ingen aning.