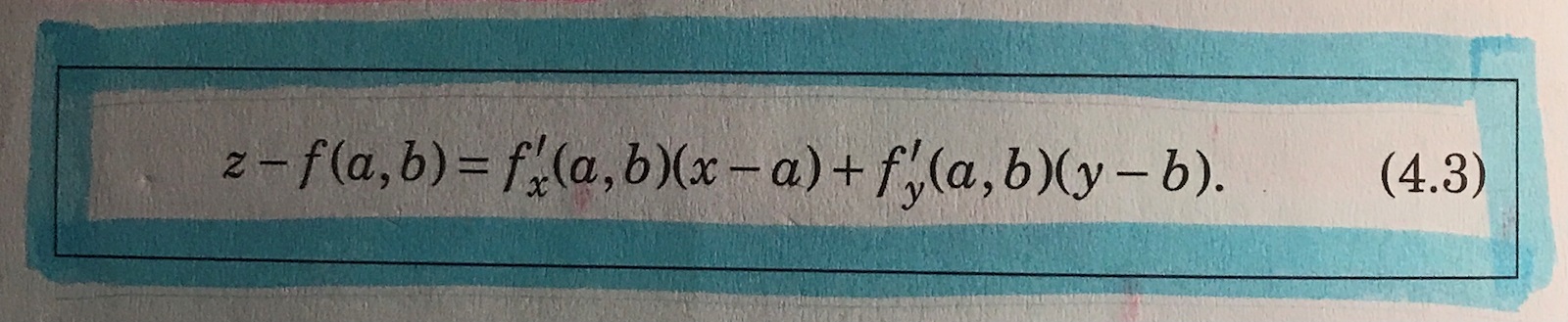Bestäm alla punkter på funktionsytan z=x^2+4y^2 (J.Månsson 4.6)
Hej!
Jag har lite problem med följande fråga:
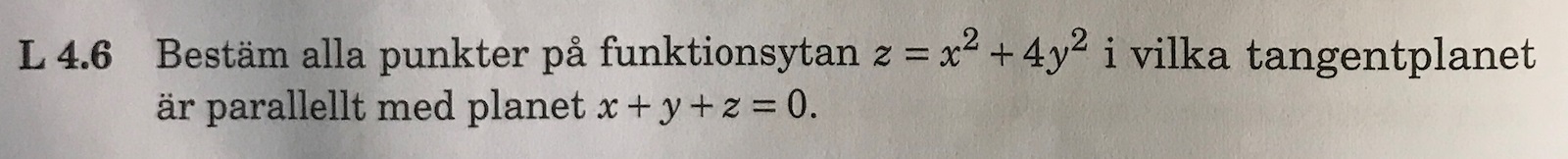
Där jag har gjort följande:
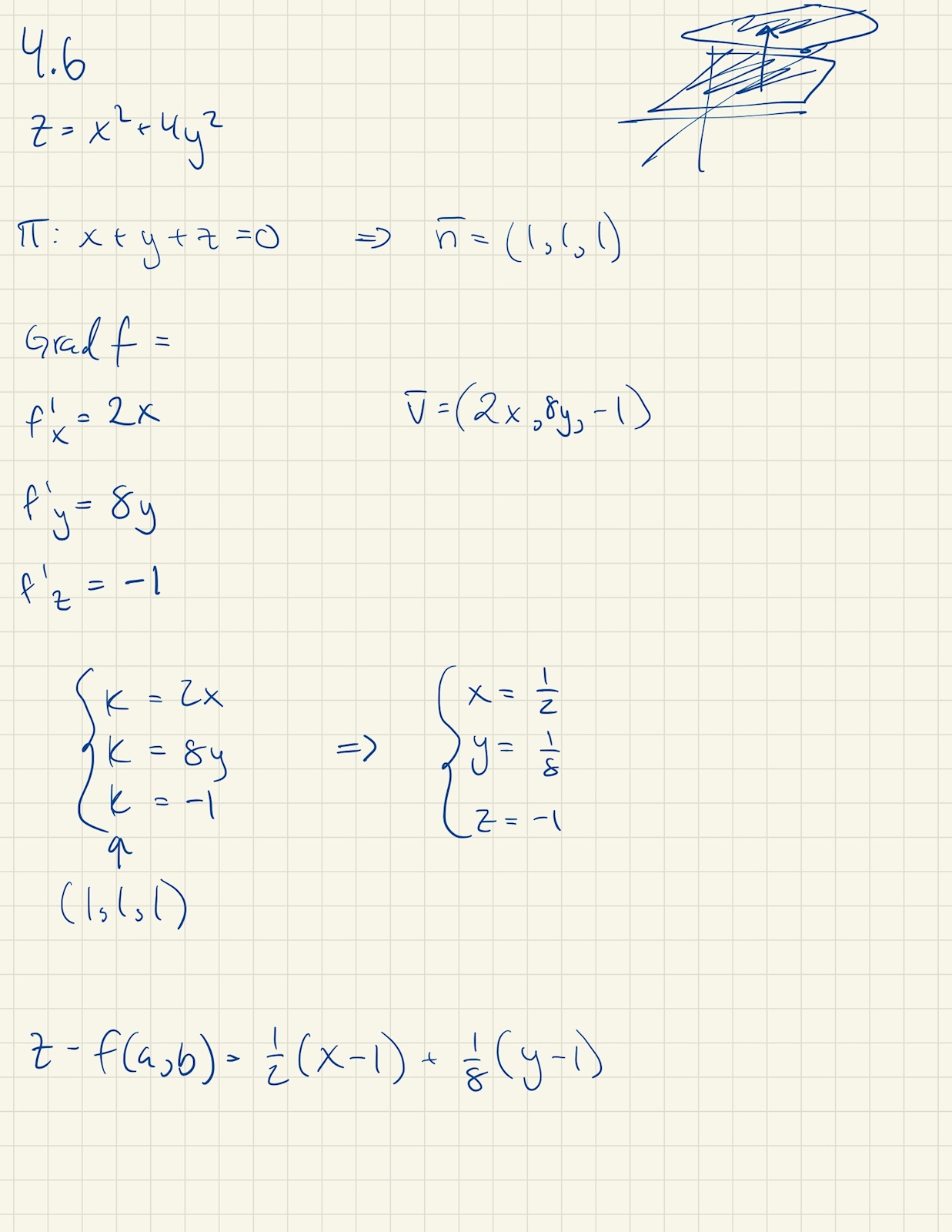
Men kommer inte riktigt vidare härifrån (kollat facit och mitt plan verkar vara fel men ser inte riktigt vart...)
Kan det vara fel med funktionsytans normalvektor?
Om man har en funktionsyta
är normalvektorn
Notera att din normalekvation endast ger dig värden på x och y. Du sätter z = k = -1. Men du har inget fog för detta. Gå tillbaka till ekvationen för funktionsytan och räkna ut z-värdet svarande mot de värden på x och y som du tagit fram.
@MaKe / PANTENTERAMERA
Humm, men borde inte gradienten av f bli normalvektorn för f?
I punkten är normalvektorn
.
Finns en enklare metod i det här fallet:
Visa spoiler
Alla plan parallella med är på formen , där är ett godtyckligt reellt tal. Så man vill finna det så att ekvationssystemet , har en unik lösning. Men
Så ger den unika lösningen , .
MaKe skrev:I punkten är normalvektorn
.
Hummmm..... Har hittat sidan i boken som är det jag tänker på:

Den ger lite annat svar (eller fel riktning)...
Darth Vader skrev:Finns en enklare metod i det här fallet:
Visa spoiler
Alla plan parallella med är på formen , där är ett godtyckligt reellt tal. Så man vill finna det så att ekvationssystemet , har en unik lösning. Men
Så ger den unika lösningen , .
Intressant tilltägg men är inte riktigt med på
Det verkar att du blandar ihop funktionsytor och nivåytor .
Notera också att en normalvektor inte är given entydigt. Har man en normalvektor, så kan den multipliceras med ett nollskilt tal och så får man en annan normalvektor.
I inlägget #4 skriver du att grad f är normalvektorn då . Det stämmer inte riktigt:
- För det första ska vara en funktion om "" ska vara meningsfullt. Du har angett att är en ekvation, vilket innebär att är ett odefinierat objekt. Om du skriver om ekvationen till , så kan du definiera funktionen för att beskriva ytan som en nivåyta . Med en sådan funktion är meningsfull och då blir verkligen en normalvektor till tangentplanet.
- För det andra är grad f inte normalvektorn utan bara en av möjliga normalvektorerna.
Som PATENTERAMERA skrivit i inlägget #3, så har du felaktigt satt z=-1. I ekvationssystemet
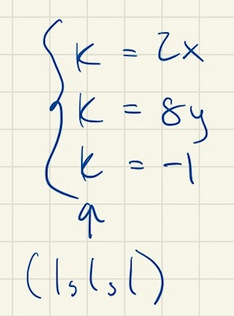
ser man bara att , och . (Lägg märke till minustecken för och ). Detta ekvationssystem säger absolut ingenting om vad skall vara. Värdet på bestäms utifrån ytans ekvation genom att sätta in de funna värdena på och . Dessa blir koordinaterna för tangeringspunkten.
När du hittat tangeringspunkten, så kan du ta fram tangentplanetsekvation på normalform:
där ettorna framför varje av parenteserna kommer från och är tangeringspunktens -koordinat som du får beräkna enligt stycket ovan.
Alternativ lösning:
Om du betraktar ekvationen som en funktionsyta , där , så får du att är en normalvektor. Ur ekvationssystemet som tidigare får du att , är - och -koordinaterna för tangeringspunkten. Då kan tangentplanet skrivas på formen av "förstaordningens taylorutveckling":
Wow! Tack för den utförliga förklaringen! Är nu dock inte riktigt med på hur jag ska få fram värdena på x,y för att stoppa in dem i blir det ett ekv. med endast ?
Om planets normal ska vara parallell med normalen till ytan ska alltså
där
Normaler till planet ges av för olika värden på . På det sättet behöver vi inte bry oss om "längden" på normalen.
Uttrycket är ett ekvationssystem med tre ekvationer och tre okända, och
Det har lösningarna , samt .
Du satte nästan upp det korrekta ekvationssystemet i ditt första inlägg, enda problemet var att du blandade in .
-koordinaten för tangeringspunkten ges slutligen av
Humm, har lite svårt att greppa z-koordinaten eller i alla fall härledning utav den har det med följande att göra?
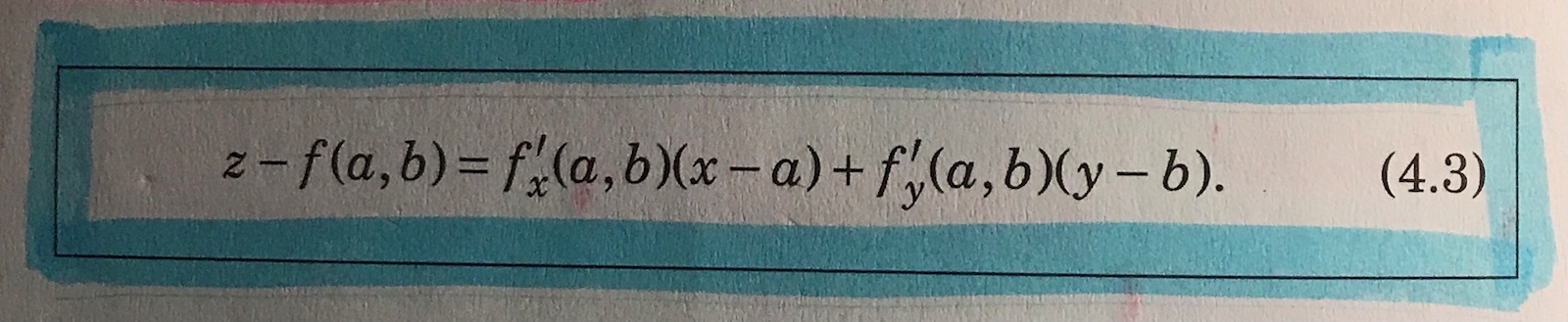
(Försöker att koppla det till vad som sägs i boken, men får kanske ge upp på det hahaha)
ChocolateTerrain skrev:Humm, har lite svårt att greppa z-koordinaten eller i alla fall härledning utav den har det med följande att göra?
(Försöker att koppla det till vad som sägs i boken, men får kanske ge upp på det hahaha)
Detta är ju exakt det jag skrivit i slutet av den alternativa lösningen i inlägget #9 (fast jag kallade funktionen för g):
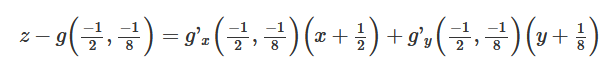
Bokstäverna och i formeln (4.3) i boken representerar - och -koordinaterna av tangeringspunkten, så i denna konkreta uppgift är och eftersom det är just i denna punkt som normalvektorn till ytan, d.v.s. , är parallell med normalvektorn till det givna planet, d.v.s. .
Värdet av anger då -koordinaten av tangeringspunkten på ytan då och .
Ahhh! Tack!
Här kommer en alternativ lösning:


Går däremot emot #3 men övningsledaren gav rätt för att k=-1.