Bestäm area av triangel

Jag skulle börja med att rita. (Jag gjorde det nyss, för att förstå vad jag håller på med.)

Sedan skulle jag se om jag inte kan hitta skärningspunkten för linjerna.

Jag ritade för linjerna Y = x och y = 4-x. Och skärningspunkten är ju då x = 2.

Sedan b flyttar ju både skärningspunkten och längden på triangelns bas hur som helst..

Nej, det är för svårt, grejar det inte. Hoppar uppgiften. Tack iaf.

Jag ritade en bild här: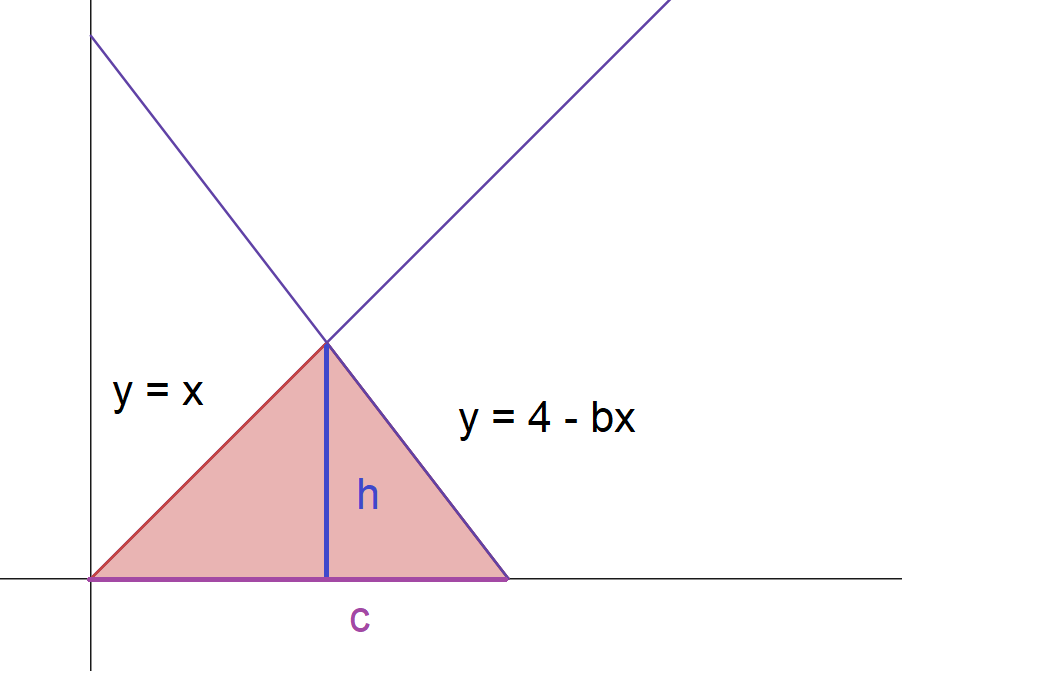

Här döptes höjden på triangeln till $h$ och basen till $c$ ($b$ är ju upptaget). Hur kan vi beräkna höjden $h$ och basen $c$? Några viktiga punkter relaterade till dem?

Då tar jag lösningen i mål ändå. Läs om du vill. 

Ekvationssystemet ovan ger oss ett uttryck för y, alltså vår höjd i skärningspunkten:

$y=\frac{4}{b+1}, b\ne -1$

Triangelns höjd är alltså: $h=\frac{4}{b+1}$

Var skär linjen x-axeln, jo där y=0. Vi petar in en nolla i linjens ekvation:

$$\begin{gathered} y=4-bx, y=0 \\ 0=4-bx \\ bx=4 \\ x=\frac{4}{b} \end{gathered}$$

Då kan vi ställa upp en ekvation för arean:

$A=\frac{{\displaystyle \frac{4}{b}}\times {\displaystyle \frac{4}{b+1}}}{2}=\frac{{\displaystyle \frac{16}{b^2+b}}}{2}=\frac{16}{2(b^2+b)}=\frac{8}{b^2+b}$

Vi vill veta när A=18:

$$\begin{gathered} 18=\frac{8}{b^2+b} \\ 18(b^2+b)=8 \\ 18b^2+18b-8=0 \\ {b}_1=-\frac{4}{3} \\ \boxed{b_2=\frac{1}{3}} \end{gathered}$$

Höjden är skärningspunkten mellan som beror av b och basen c beror också på b.

Så ena hörnet är x = 0 eftersom x axeln utgör c och y = x skär i origo.

Andra hörnet på x axeln är när y = 4-bx är = 0. som beror på b. Så b = 4/x 

Sen höjden är när linjerna skär så 4-bx = x. Så löser man ut b, b = (-x+4)/x.

Kanske. 

Sen vill vi då att ((4/x) ((-x+4)/x))/2 = 18

Okej tack 👍