Bestäm arean

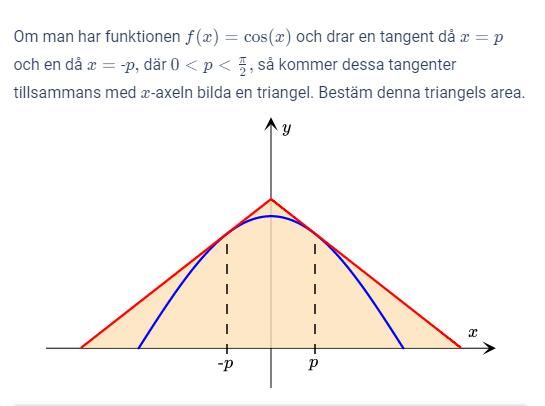
Pga symmetrin räcker det att bestämma högra halvan av triangeln. Bestäm ekvationen för tangenten i punkten (p, cos p) Höjden är tangentens  skärning med y-axeln och basen är tangentens skärning med x-axeln. Dubblera för att få hela arean. 

jag får arean att bli (2p*cos(p)) + (sin(p)p²) - (cos²(p)/sin(p))

Jag får samma termer fast utan minustecken.

Ja, får också det nu. Det blir dock fel när jag skriver in det som svar, tror du de vill ha ett numeriskt värde och är det ens möjligt att få ett antar att det kan variera då flera p-värden bör funka

Ett numeriskt värde skulle innebära att arean är oberoende av p, men din areafunktion som du tagit fram är icke-konstant, så det är omöjligt.

Men är mitt uttryck korrekt, blir som sagt fel när jag skriver in det, har försökt skriva om det också

Pröva att skriva den sista termen som cos(p)*cot(p)

blir också fel

Vi kan skriva om resultatet på andra sätt, t.ex. genom att bryta ut $\sin(p)$.

Vi får då

$\sin(p)\cdot (p^2+2p\cdot\cot(p)+\cot^2(p))$

Vilket i sin tur kan skrivas om till

$\sin(p)\cdot (p+\cot(p))^2$.

Men det är lite långsökt.

Kanske har vi tänkt fel, finns det någon annan som har ett bättre svar?

jag kommer fram till samma uttryck, problemet kanske är att svaret går att skriva om på i stort sett hur många sätt som helst och det är omöjligt att veta vilken variant facit tycker är rätt.