Bestäm arean av det gråa området

Jag har försökt tänka när

$$\begin{gathered} y_1=2\sin (x-\frac{\mathrm{\pi }}{4})=0 \\ 2\sin (x-\frac{\mathrm{\pi }}{4})=0 \\ \sin (x-\frac{\mathrm{\pi }}{4})=0 \\ ar\sin \left(\sin \right(x-\frac{\mathrm{\pi }}{4}\left)\right)={\sin }^{-1}\left(0\right) \\ x-\frac{\mathrm{\pi }}{4}=0 \\ {x}_1=\frac{\mathrm{\pi }}{4} \\ {x}_2=\frac{3\mathrm{\pi }}{4} \end{gathered}$$

${\int }_{\frac{\mathrm{\pi }}{4}}^{\frac{3\mathrm{\pi }}{4}}\left(2\sin \right(x-\frac{\mathrm{\pi }}{4})dx={{\left[-2\cos (x-\frac{\mathrm{\pi }}{4}\right]}_{\frac{\mathrm{\pi }}{4}}}^{\frac{3\mathrm{\pi }}{4}}$

Tillägg: 31 jan 2026 17:16

det här fick jag till -2,78 enligt min grafräknare

Arup skrev:

${\int }_{\frac{\mathrm{\pi }}{4}}^{\frac{3\mathrm{\pi }}{4}}\left(2\sin \right(x-\frac{\mathrm{\pi }}{4})dx={{\left[-2\cos (x-\frac{\mathrm{\pi }}{4}\right]}_{\frac{\mathrm{\pi }}{4}}}^{\frac{3\mathrm{\pi }}{4}}$

---

Tillägg: 31 jan 2026 17:16

det här fick jag till -2,78 enligt min grafräknare

Då ytan till största delen ligger ovanför x-axeln skall integralen > 0.

Uppg-nr. har en ruta = räknaruppgift. Tror inte du skall lösa så många ekvationer utan till stor del rita och låta räknaren beräkna allt. Det finns inbyggda funktioner för allt detta.

Vad bör jag få skriva på min räknare ?

jag har ti 84 plus ce

Arup skrev:

jag har ti 84 plus ce

På min CG50 angav jag de två funktionerna, ritade dem, frågade efter integralen mellan 2 skärningspunker och den svarade 4. Vilket är rätt svar. Tog under 1 minut. Imponerande pryl.

Hur kan vi få så olika ?

Arup skrev:

Hur kan vi få så olika ?

Om du lägger upp bilder på vad du gör så kan nog någon TI-expert säga vad som är felet.

våra modeller är ju de mest avancerade på marknaden så borde inte det ge mig rätt svar på ett svep ?

Vilka slutsatser kan dras av bilden?

Är det OK att flytta A och B så att funktionerna blir 2sinx och sin2x

Kan man säga att det grå området helt enkelt blir 

$2{\int }_0^{\pi }\sin xdx$

Hansa jag förstår inte riktigt vad du menar

$2 \sin \left(x\right)$är inte samma sak som $\sin \left(2x\right)$

Arup skrev:

våra modeller är ju de mest avancerade på marknaden så borde inte det ge mig rätt svar på ett svep ?

Så här gör jag på CG50

-- Def. Y1=2sin(x-π/4), Y2=-cos(2x)

-- Ritar graferna

-- Solve > Integral > Intersect  (går till vänster skärningspunkt, markerar, går till höger skärningspunkt, markerar)

CG50 skuggar korrekt område och svarar att arean är 4 a.e. Klart.

Så tror jag denna uppgift är avsedd att lösas.

Den kan lösas för hand, men varför är den då inrutad?

Klart man kan ta fram det tunga artilleriet men det har man inte skolan;

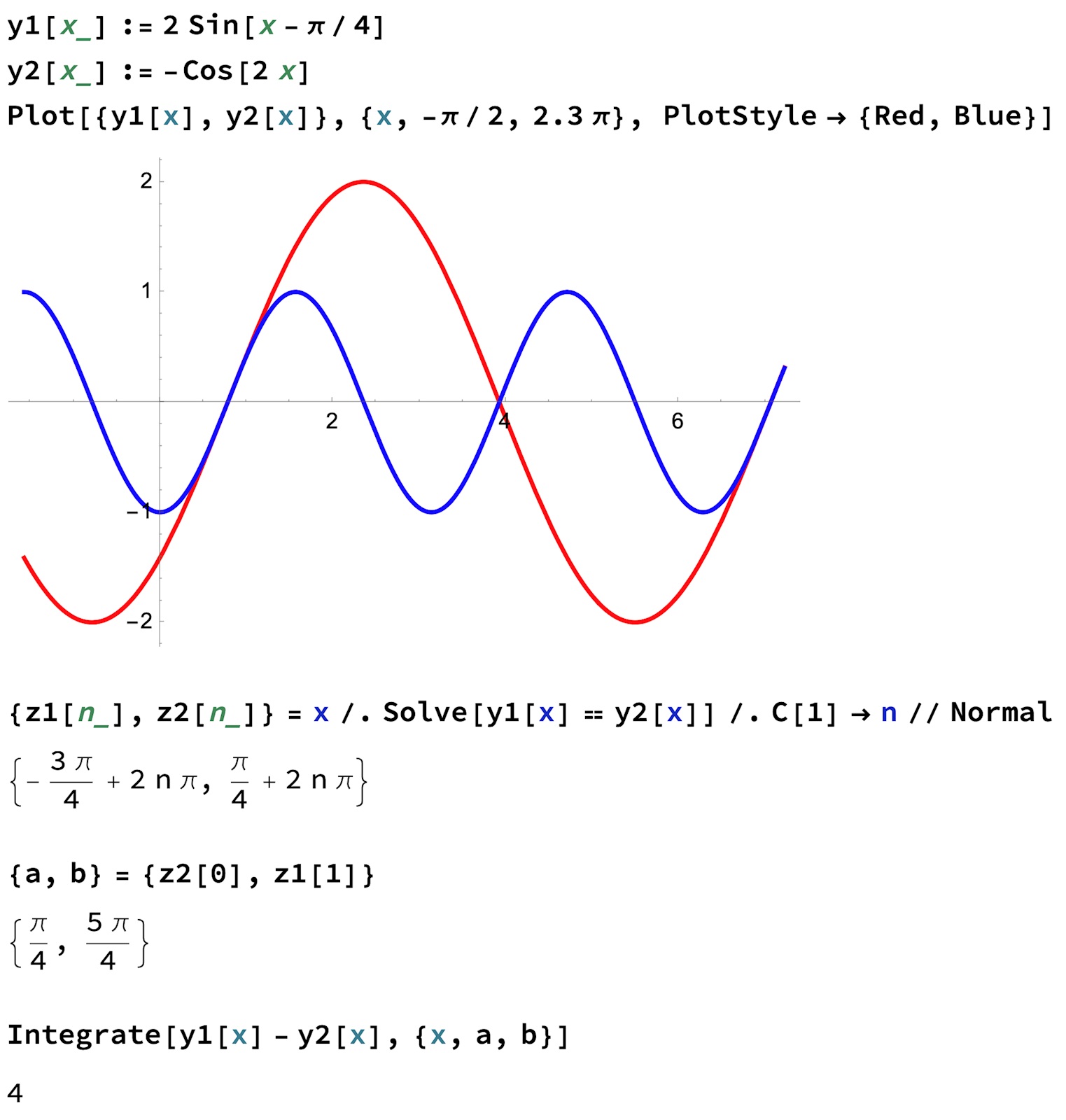
Dessutom är metoden i CG50 föredömligt enkel, och snygg.

Så här blev det för mig för sinus funktionen

Arup skrev:

Så här blev det för mig för sinus funktionen

1/4 π --- 3/4 π är denna bit

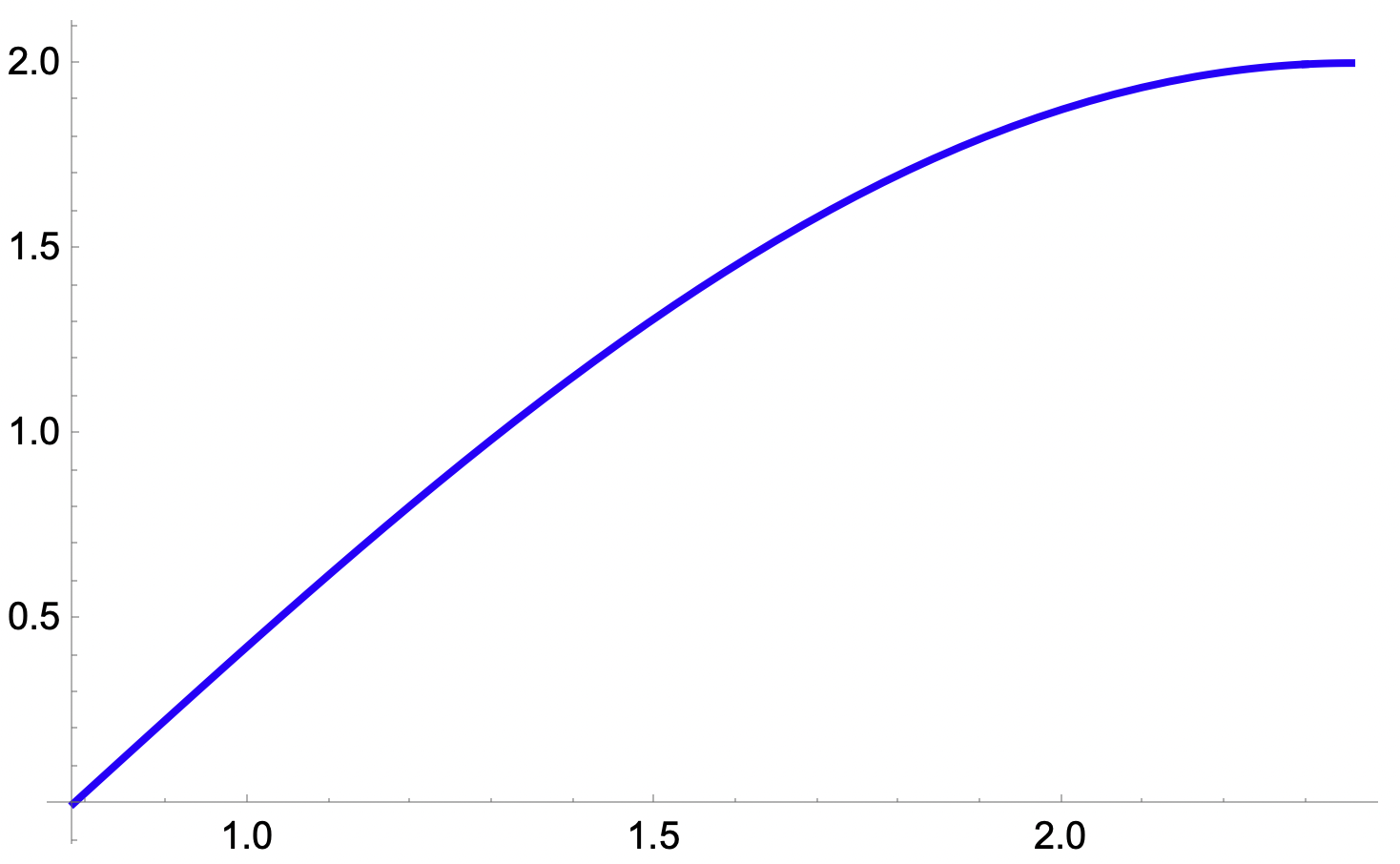
men det är inte det som efterfrågas.

Variabeln x ska inte multipliceras med vinkeln -pi/4. Man ska helt enkelt subtrahera pi/4 från x.

Sedan så är övre integrationsgränsen 3pi/4 inte korrekt. Det borde ha varit 5pi/4.

varför ska den övre gränsen vara $\frac{5\mathrm{\pi }}{4}$och inte$\frac{3\mathrm{\pi }}{4}$?

Det här stämemr inte riktigt.

Ekvationen sin(x-pi/4) = 0 har lösningarna

x₁ - pi/4 = 0 + n*2pi

x₂ - pi/4 = pi + n*2pi

Räkna vidare från det.

just det jag glömde att den 2:a lösningen skulle subtrahera med pi radianer alt 180(grader)