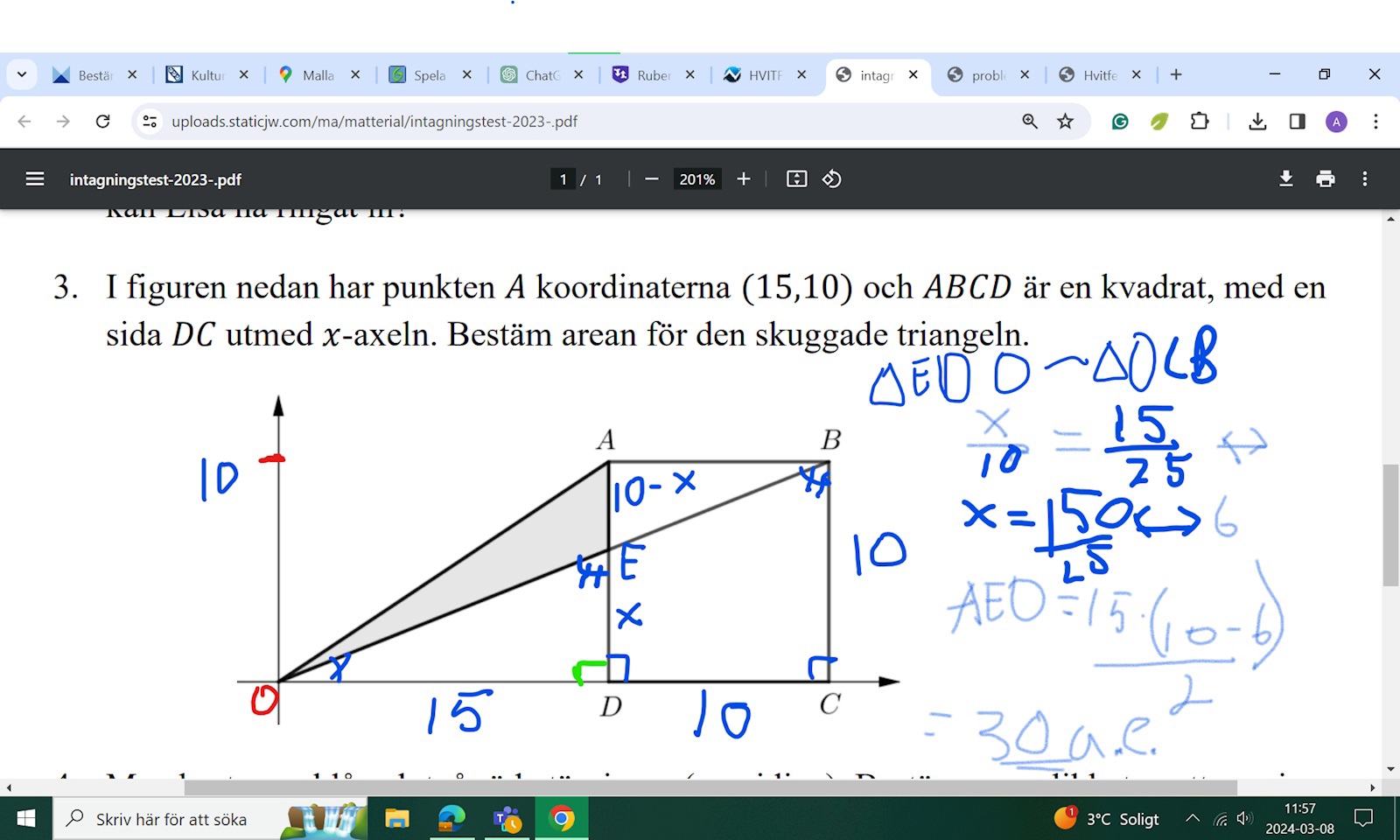
Bestäm arean för den skuggade triangeln
Skulle man kunna använda pythagoras eller rita en vinkelrät linje linje från hörnet C som en början ? På uppgift 3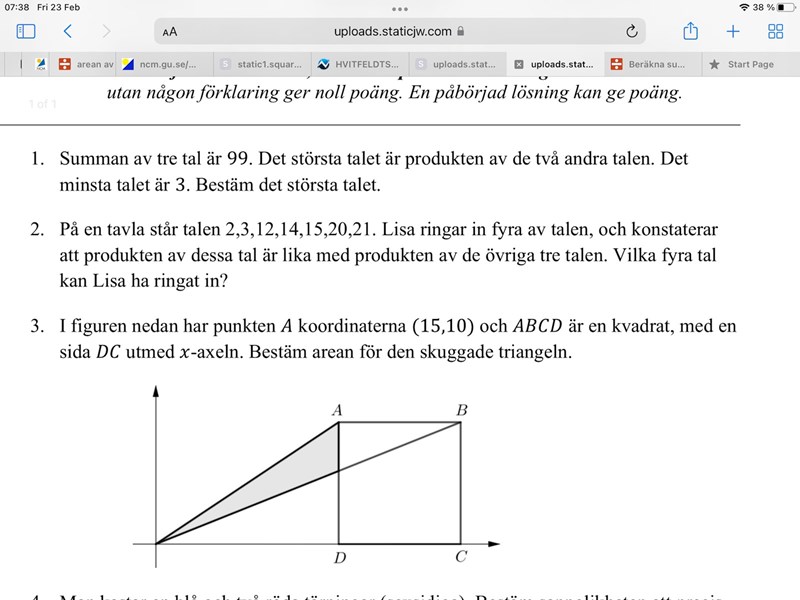
Hej.
Om du kallar hörnet i origo för O och skärningen mellan OB och AD för E så kan du beräkna arean av triangeln OAE som arean av trianeln OAD plus arean av kvadraten ABCD ninus arean av triangeln ABE.
Ok . Jag kör på det
Yngve, det där får jag inte att gå ihop.
Man kan beräkna DE med likformighet, därmed också AE.
Då har vi både bas (AE) och höjd (OD) i triangel OAE och kan beräkna arean direkt.
Louis skrev:Yngve, det där får jag inte att gå ihop.
Vad är det som inte stämmer?
Man kan beräkna DE med likformighet, därmed också AE.
Då har vi både bas (AE) och höjd (OD) i triangel OAE och kan beräkna arean direkt.
Det är en smartare lösning 👍
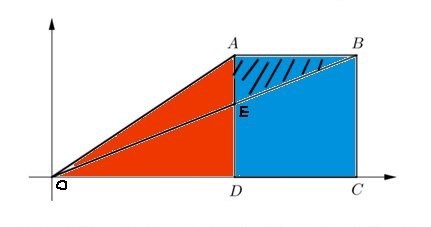
"Om du kallar hörnet i origo för O och skärningen mellan OB och AD för E så kan du beräkna arean av triangeln OAE som arean av triangeln OAD (röd)
plus arean av kvadraten ABCD (blå) = hela figuren
minus arean av triangeln ABE. (streckad)"
Är det någon beteckning som inte stämmer? Eller något som fattas (som minus OBC)?
Ojdå, jag både krånglade till det och skrev fel. Glöm mitt inlägg.
kan man rita en "hjälp linje" i så fall var ska den ritas nånstans ?
Kanske det, men jag ser inte hur det skulle underlätta.
Använd tipset som Louis gav i svar #4.
Det ger en snabb och smidig lösning.
löst det