Bestäm argumentet i radianer och exakta värdet på absolutbeloppet
Hej, har kört fast på en övning, skulle uppskatta något tips, säkert något dumt slarvfel.
Bestäm argumentet i radianer och exakta värdet på absolutbeloppet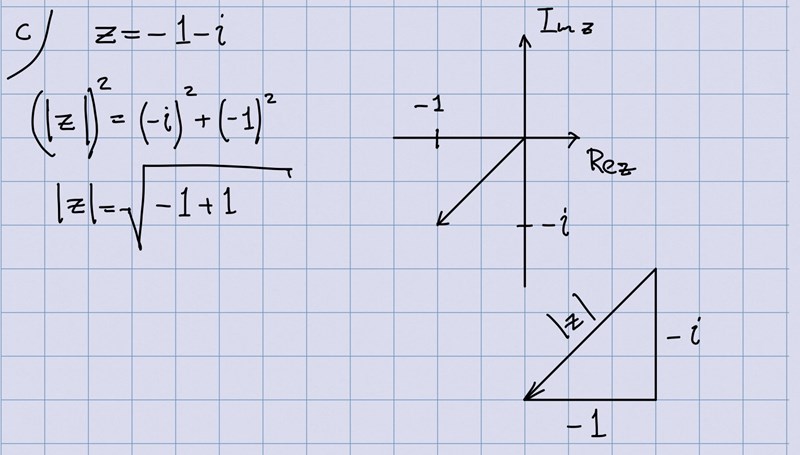
Facit:
Argumenten är vinkeln som skapas då vektorn vrids från positiva x-axeln till där den är nu. Du kan använda tangens för att bestämma vinkeln mellan vektorn och negativa x-axeln och argumentet är detta adderat med...? Kan du fortsätta härifrån?
Gällande absolutbelopp så finns formeln i formelbladet, och här: https://www.formelsamlingen.se/alla-amnen/matematik/komplexa-tal/absolutbelopp
När du tar kvadratroten som du gjorde ur två kvadrerade tal så funkar det inte när dessa tal är med i addition eller subtraktion. Därav ska det bli:
Hehe jag hoppas jag lyckades förklara så tydligt jag kan men återkom gärna vid funderingar
Om det komplexa talet skrivs på formen så räknar man ut absolutbeloppet enligt . Notera att det inte finns något i under rottecknet.
I ditt fall blir det alltså
Tegelhus skrev:Om det komplexa talet skrivs på formen så räknar man ut absolutbeloppet enligt . Notera att det inte finns något i under rottecknet.
I ditt fall blir det alltså
Tack ska ni båda ha!


