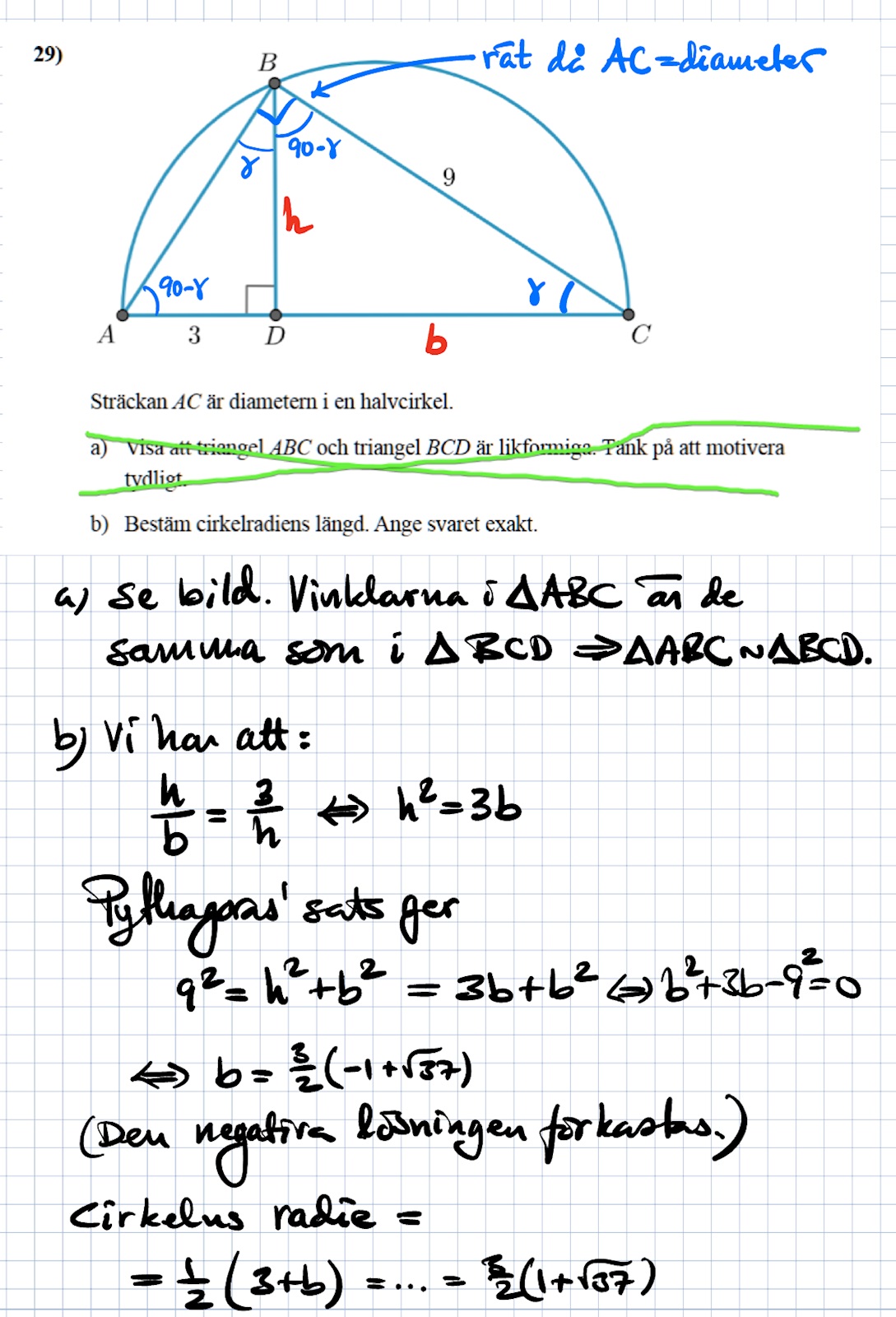
Bestäm cirkelradiens längd
Hejsan! Jag har nu suttit med b) i ett tag nu, men jag kan verkligen inte få någon början, så jag tänker att jag frågar här!
Gissningsvis tänker jag att det kommer bli likformigheter mellan vissa sidor i triangel ABC och triangel BDC, men vet inte vilka, någon som kan hjälpa?
Titta ordentligt så kommer du att se att alla tre trianglarna är likformiga med varandra.
De har samma uppsättning hörnvinklar ....
Arktos skrev:Titta ordentligt så kommer du att se att alla tre trianglarna är likformiga med varandra.
De har samma uppsättning hörnvinklar ....
Går det att sätta upp det som 3/(AC-3) = 9/AC ?
(AC-3 från triangeln DBC)
9/AC är [lång katet] / [hypotenusa] i ∆ABC
men 3 och (AC-3) är inte två sidor i samma triangel.
Så det går inte
Arktos skrev:9/AC är [lång katet] / [hypotenusa] i ∆ABC
men 3 och (AC-3) är inte två sidor i samma triangel.
Så det går inte
i 9/AC är 9 hypotenusa för triangeln DBC och AC är hypotenusa för ABC, bör inte det funka då? (får dock fel svar)
Tillägg: 20 nov 2025 23:42
vänta lite här nu, inser att jag har skrivit upp triangeln ABD fel, så att fel sidor blir motsvariga varandra
DB är väl motsvarigheten till DC eller?
Tillägg: 20 nov 2025 23:46
deeeettt var inget, inser att jag har ritat upp allting fel, så konstigt att sitta och vända på trianglar för att försöka få dom att stå på långa kateten, allihopa
I DBC är 9 hypotenusa, DB kort katet och CD lång katet
I ∆ABC är 9 lång katet , AC hypotenusa och AB kort katet
3 är kort katet i ∆ABD
(AC - 3) = CD är lång katet i ∆BCD
Det är inte samma triangelpar, så det går inte.
Vad knepigt detta är med ord!
Förhållandet mellan två sidor i en av dessa trianglar
är lika med
förhållandet mellan motsvarande sidor i de övriga trianglarna
Okej nu får vi se ifall jag har ritat upp rätt
Hypotenusan i ABC är AC, kort katet är AB, lång katet är BC (längd 9)
Hypotenusan i ABD är AB, kort katet är AD (längd 3), lång katet är DB
Hypotenusan i BDC är BC (längd 9), kort katet är BD, lång katet är DC
känns som att det går ganska enkelt att lösa nu, eller?
Det är nog rätt.
Jag blir lite vindögd av skrolla tillbaka tlll figuren ideligen.

Om det är knepigt med ord kan det i geometriuppgifter ofta vara till hjälp med en figur
Mycket bra!
Hypotenusa / Lång katet
i två av trianglarna
är nog bäst här, men kan ta tid att komma på
Ska bara försöka spika fast det i huvudet vilka sidor i vilka trianglar jag borde gå på... väldigt svår uppgift (tyckte jag iallafall)
Visa spoiler
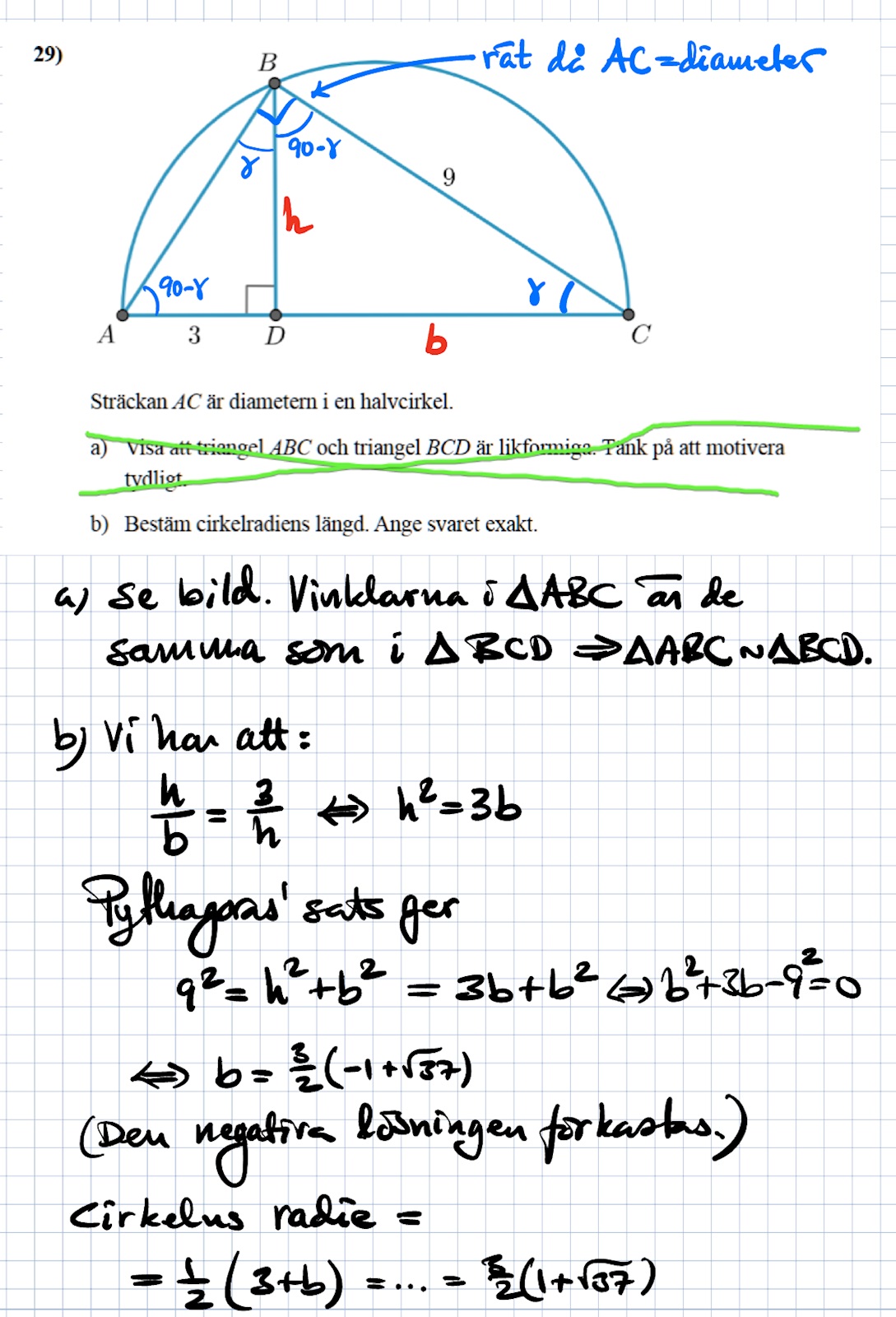
blir det alltså AC/BC = BC/DC för att sedan få AC?
Tillägg: 21 nov 2025 00:21
ja det blev det !!!! äntligen, vi får alltså AC/9 = 9/(AC-3)
(BC är 9, och DC är AC-3)
och vi kan då lösa för AC för att få AC^2 - 3AC - 81 = 0 (lös med PQ)
för att få AC = 1.5+√(2.25+81), negativ lösning bortser vi ifrån
och AC/2 är radien, alltså (1.5+√(83.25))/2, vilket är svaret (inte exakt som i facit, men det ger samma värde)
Trinity2 skrev:Visa spoiler
Dock en intressant lösning här som jag får titta på senare, måste få i mig sömn innan provet :)
Lös Hansas ekvation så får du lätt exakt värde
Trinity har ett annat förslag.
Roligt att se flera lösningar till samma problem :-
Välkommen till Pluggakuten, KanskeSmart!