Bestäm de komplexa tal med belopp 1 för vilka det gäller att |1+iz| = 1
Hej! Jag förstår inte riktigt hur de kom fram till svaret i facit?
Frågan lider:
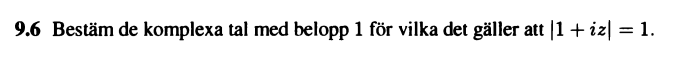
Facit:
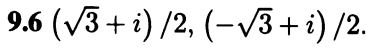
Tack på förhand!
Sätt z = a+bi, där vi vet att |z| = 1, dvs att a2+b2 = 1.
Då är iz = i(a+bi) = ai+bi2 = -b+ai
Vi vill nu bestämma alla möjliga värden på a och b som dessutom uppfyller att |1+iz| = 1, dvs att |1-b+ai| = 1.
Kommer du vidare då?
Man kan också prova en mer geometrisk variant. Att |z|=1 betyder att z ligger på enhetscirkeln. Då ligger också iz på enhetscirkeln. Dess avstånd till punkten -1 ska vara 1, vilket betyder att iz också ska ligga på cirkeln med medelpunkt i -1 och radien 1. Där den cirkeln skär enhetscirkeln har vi punkterna för iz. Därur får man var z ska ligga. ( jmf konstruktion av en liksidig hexagon Mh a passare och linjal)
Tack för svaren!
om vi ska bestämma värdena för a och b då |1-b-ai| = 1 får vi:
(1-b)^2 + (a)^2 = 1 <=> 1-2b+b^2 + a^2 = 1 <=> b^2 + a^2 -2b = 0
Vet inte om jsg tänkt rätt så lång och om så hur jag ska fortsätta?:(
Du har även att a2 + b2 = 1. Utnyttja det i din sista ekvation.
Ah juste tack! Då får jag att a =+- /2 och b = 1/2:
b^2 + a^2 - 2b = 0 (1)
a^2 + b^2 = 1 <=> a^2 = 1- b^2 (2)
(2) i (1): b^2 + 1 - b^2 - 2b = 0 <=> 2b = 1 <=> b = 1/2
från (2): a^2 = 1 - b^2 <=> a = <=> a = <=>a=+- /2
Det stämmer med svaret i facit. Bra!
Tack för hjälpen!


