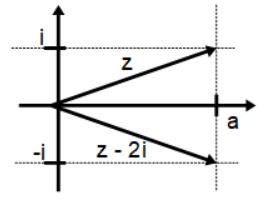
bestäm de z som uppfyller ekvationen

Börja med att försöka översätta uttrycket till ren svenska. Avståndet mellan punkten $z$ och punkten 2i skall vara lika stort som...

Smaragdalena skrev:

Börja med att försöka översätta uttrycket till ren svenska. Avståndet mellan punkten $z$ och punkten -2i skall vara lika stort som...

.. som abs z

men vad är abs z ?

z = a+bi 

(a+bi) - 2i = a+bi ?

ser krångligt ut, hittar inga siffror

Du söker alla punkter som ligger lika långt från punkten 0+2i som från punkten 0+0i. Alla dessa punkter kommer att ligga på en rät linje.

Smaragdalena skrev:

Du söker alla punkter som ligger lika långt från punkten 0+2i som från punkten 0+0i. Alla dessa punkter kommer att ligga på en rät linje.

Rita!

Rita upp punkterna 0+2i och 0+0i. Vilken punkt ligger mitt emellan dem? Vilken punkt med realdelen 5 ligger lika långt från båda? Vilken punkt med realdelen -7 ligge rlika långt från båda? Siffrornaär slumpmässiga, tycker du bättre om några andra så använd dem istället.

okej men  vart kommer 0 från? alltså 0 + 2i och 0+0i?

okej men vart kommer 0 från? alltså 0 + 2i och 0+0i?

Från |z-2i| respektive |z|.

Smaragdalena skrev:

okej men vart kommer 0 från? alltså 0 + 2i och 0+0i?

Från |z-2i| respektive |z|.

är z alltid = med 0 eller hur vet man att det är så just här?

|z| betyder absolutbeloppet av z, d v s avståndet från origo till z i det komplexa talplanet.

|z-2i| betyder absolutbeloppet av z-2i, d v s avståndet från punkten z-2i till origo eller avståndet från punkten z till punkten 0+2i.

Smaragdalena skrev:

|z| betyder absolutbeloppet av z, d v s avståndet från origo till z i det komplexa talplanet.

|z-2i| betyder absolutbeloppet av z-2i, d v s avståndet från punkten z-2i till origo eller avståndet från punkten z till punkten 0+2i.

okej okej

så avståndet från punkten z-2i till origo är lika med avståndet från origo till z, om man ska översätta ekvationen?

Maremare skrev:

okej okej

så avståndet från punkten z-2i till origo är lika med avståndet från origo till z, om man ska översätta ekvationen?

Nej.

Smaragdalena skrev:

Du söker alla punkter som ligger lika långt från punkten 0+2i som från punkten 0+0i. Alla dessa punkter kommer att ligga på en rät linje.

Rita!

Rita upp punkterna 0+2i och 0+0i. Vilken punkt ligger mitt emellan dem? Vilken punkt med realdelen 5 ligger lika långt från båda? Vilken punkt med realdelen -7 ligge rlika långt från båda? Siffrornaär slumpmässiga, tycker du bättre om några andra så använd dem istället.

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Maremare skrev:

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Ja, det blir det och du kan skriva det som $x+i(y-2)$, precis som jag gjort. 

Albiki skrev:

Maremare skrev:

Visa föregående citat

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Ja, det blir det och du kan skriva det som $x+i(y-2)$, precis som jag gjort. 

aa okej, sen då? det finns ju inga siffror, vad är det jag ska lösa ut för att markera i talplanet? är förvirrad

Om du tycker att Albikis tips är svårt att fortsätta med, så titta på Smaragdalenas alla svar igen samtidigt som du funderar på din bild av komplexa talplanet. Jag tror att du kommer att förstå. Det blir en tydligt geometrisk uppgift. Avstånd vet vi alla vad det är.

Maremare skrev:

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Naturligtvis, och när vi samlar imaginärdelen tillsammans (allt med i) så blir det x + iy - 2i = x + (y-2)i.

Laguna skrev:

Maremare skrev:

Visa föregående citat

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Naturligtvis, och när vi samlar imaginärdelen tillsammans (allt med i) så blir det x + iy - 2i = x + (y-2)i.

yes nu är jag med på det. men vad är steget efter det? 

ska man på något sätt bryta ut x och yi för att se vilka konstanter som ska ersättas för att få till ekvationen eller?

Maremare skrev:

Laguna skrev:

Visa föregående citat

Maremare skrev:

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Naturligtvis, och när vi samlar imaginärdelen tillsammans (allt med i) så blir det x + iy - 2i = x + (y-2)i.

yes nu är jag med på det. men vad är steget efter det? 

ska man på något sätt bryta ut x och yi för att se vilka konstanter som ska ersättas för att få till ekvationen eller?

Du kan ju fortsätta från det som Albiki började. 

Laguna skrev:

Maremare skrev:

Visa föregående citat

Laguna skrev:

Maremare skrev:

Visa föregående citat

Albiki skrev:

Hej!

Du skulle också kunna se vad ekvationen säger om talen $x$ och $y$ då du skriver $z$ på rektangulär form $z=x+iy.$

Det gäller att $z-i2 = x+i(y-2)$ så dess absolutbelopp är $\sqrt{x^2+(y-2)^2}.$ Detta ska vara lika med absolutbeloppet $\sqrt{x^2+y^2}.$

    $\sqrt{x^2+(y-2)^2} = \sqrt{x^2+y^2}.$ 

om z = x + iy så borde väl z - 2i bli (x+iy)-2i ?

Naturligtvis, och när vi samlar imaginärdelen tillsammans (allt med i) så blir det x + iy - 2i = x + (y-2)i.

yes nu är jag med på det. men vad är steget efter det? 

ska man på något sätt bryta ut x och yi för att se vilka konstanter som ska ersättas för att få till ekvationen eller?

Du kan ju fortsätta från det som Albiki började. 

det kan jag dessvärre inte eftersom att jag ställde en fråga på det han svarade med precis som jag ställde till dig då du svarade det han redan svarat

Du har en ekvation med kvadratrot på båda sidor. Kvadrera båda sidorna och fortsätt därifrån. 

Laguna skrev:

Du har en ekvation med kvadratrot på båda sidor. Kvadrera båda sidorna och fortsätt därifrån. 

jo men det jag inte förstår är om jag ska lösa ut x ensamt eller y ensamt eller i ensamt elr x+iy ensamt eller vad ska jag lösa ut?

Lös ut y, så får du fram linjen för den räta linje som jag har talat om hela tiden. Ett snabbare sätt är att rita, som du har fått so förslag redan.

Smaragdalena skrev:

Lös ut y, så får du fram linjen för den räta linje som jag har talat om hela tiden. Ett snabbare sätt är att rita, som du har fått so förslag redan.

jag kan inte se att du sagt löst ut y, men jag ska testa det =)

återkommer med hur det gick

Nej, jag har sagt att du skall rita. Då får du linjen nästan gratis.

Hej!

Om $z$ och $w$ är två komplexa tal så är det positiva talet $|z-w|$ lika med avståndet mellan de två komplexa talen. 

• Avståndet mellan $z$ och det komplexa talet $0+i2$ är lika med det positiva talet $|z-i2|$.
• Avståndet mellan $z$ och det komplexa talet $0+i0$ är lika med det positiva talet $|z-(0+i0)| = |z|.$

Markera därför de två komplexa talen $0+i2$ och $0+0i$ på det komplexa talplanet. Uppgiften handlar om att finna alla punkter (komplexa tal $z$) i planet som ligger lika långt från dessa två punkter. 

Uppgiften beskriver att man ska illustrera...rita...å då gör jag det å får:

z = a + i

....a alla reella tal....

När det står x² + (y-2)² = x² + y² så behöver man inte fråga någon vad man ska lösa ut. Man kastar sig med glädje över en ekvation som man kan göra så mycket med med så liten ansträngning:

(y-2)² = y²
y² - 4y + 4 = y²
-4y + 4 = 0
y = 1

okej nu har jag läst alla senaste inlägg och är med på hur man ska rita upp det i talplanet efter att skrivit om uttrycket till x^2 + (y-2)^2 = x^2 + y^2

får en rak linje Im = 1

det sista jag undrar är hur jag ska uttrycka svaret, själva ritandet är ju illustrationen som uppgiften efterfrågan men de frågar även "Bestäm de z som uppfyller ekvationen..." 

behöver man svara z = ... ? kan man skriva z = i ? eller hur blir det eftersom att det inte bara är en punkt

Maremare skrev:

...

det sista jag undrar är hur jag ska uttrycka svaret, själva ritandet är ju illustrationen som uppgiften efterfrågan men de frågar även "Bestäm de z som uppfyller ekvationen..." 

behöver man svara z = ... ? kan man skriva z = i ? eller hur blir det eftersom att det inte bara är en punkt

Nej du kan inte svara z = i eftersom det endast är ett tal.

Däremot kan du svara "z = a + i, där a är ett godtyckligt reellt tal".

Affe Jkpg skrev:

Uppgiften beskriver att man ska illustrera...rita...å då gör jag det å får:

z = a + i

....a alla reella tal....

Jag gjorde inget annat än ritade. Efter första (misslyckade) skissen återstod det sedan endast ett alternativ: