bestäm den elektriska potentialen phi

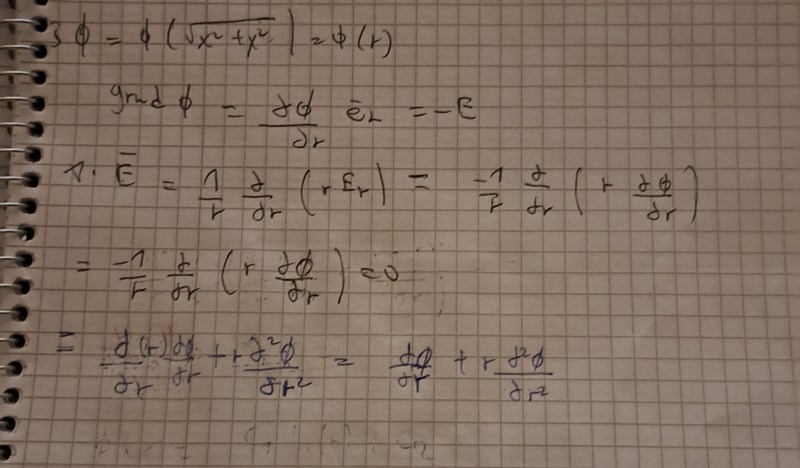
Hej!
Såhär långt har jag kommit i min lösning ovan, men är fast på hur jag ska fortsätta gå vidare med resten av lösningen. Sen vet jag inte hur man bestämmer normalriktningen till randytan så att vi får n*E=cphi
(konstant).
…
PATENTERAMERA skrev:
(konstant).…
Men det är vad jag gjort ju ?
Då får man ju dphi/d(r)=a/r och sen phi(r)=aln(r)+C2
Ja. Sedan får man använda randvillkoren för att bestämma konstanterna.
På randen så är n = er (eller möjligen -er).
Tillägg: 21 nov 2025 22:00
er.
PATENTERAMERA skrev:Ja. Sedan får man använda randvillkoren för att bestämma konstanterna.
Hur gör man detta?
PATENTERAMERA skrev:På randen så är n = er (eller möjligen -er).
Tillägg: 21 nov 2025 22:00
er.
Jag förstår tyvärr inte. vi har n*E=cphi. Hur bestämmer vi n? Varför är n=e_r?
Randen är cylinderformad. Normalen till randen är riktad in mot eller bort från z-axeln. Dvs parallell med er.
PATENTERAMERA skrev:Randen är cylinderformad. Normalen till randen är riktad in mot eller bort från z-axeln. Dvs parallell med er.
Är randen sqrt(x^2+y^2)? Hur menar du att normalen till randen är riktad in mot eller bort z axeln? Jag ser inte detta framför mig. Vad menar du med att normalen till randen är parallell med e_r?
PATENTERAMERA skrev:
Jag hänger inte med. Allt jag har förstått är att man får fram vad phi(r) blir när man integrerat från #2. #10 och #8 förstår jag tyvärr inte.
destiny99 skrev:PATENTERAMERA skrev:Randen är cylinderformad. Normalen till randen är riktad in mot eller bort från z-axeln. Dvs parallell med er.
Är randen sqrt(x^2+y^2)? Hur menar du att normalen till randen är riktad in mot eller bort z axeln? Jag ser inte detta framför mig. Vad menar du med att normalen till randen är parallell med e_r?
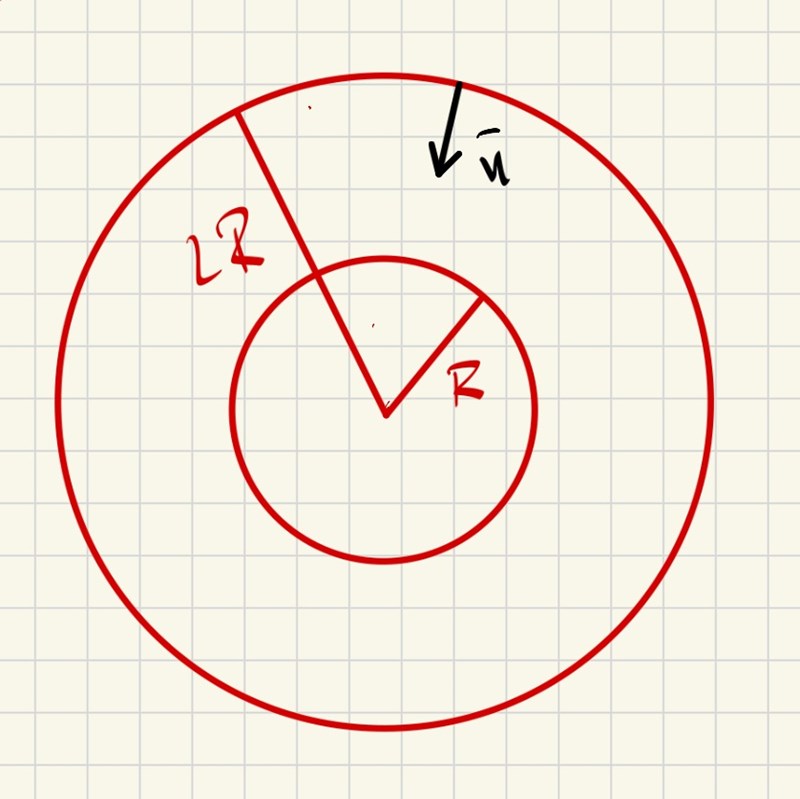
Du har två randytor. r = R och r = 2R.
Rita en figur och fundera på hur normalen ser ut till den yttre randytan.
destiny99 skrev:PATENTERAMERA skrev:
Jag hänger inte med. Allt jag har förstått är att man får fram vad phi(r) blir när man integrerat från #2. #10 och #8 förstår jag tyvärr inte.
Du har två okända konstanter i din lösning. Du bestämmer dem genom att tillse att randvillkoren blir uppfyllda.
Tillägg: 22 nov 2025 01:56
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:
Jag hänger inte med. Allt jag har förstått är att man får fram vad phi(r) blir när man integrerat från #2. #10 och #8 förstår jag tyvärr inte.
Du har två okända konstanter i din lösning. Du bestämmer dem genom att tillse att randvillkoren blir uppfyllda.
Tillägg: 22 nov 2025 01:56
Normalen är vinkelrät mot den yttre randytan. Borde vi inte ha en till normal som är vinkelrät mot den inre randytan med R?
Jo, men på den inre randytan så har vi ett annat randvillkor som inte beror på normalen. Så det fanns ingen anledning att rita ut den.
PATENTERAMERA skrev:Jo, men på den inre randytan så har vi ett annat randvillkor som inte beror på normalen. Så det fanns ingen anledning att rita ut den.
Ok. Juste den randvillkor är ju phi0. Men jag vet inte hur vi ska gå vidare från #3 och hantera n*E som har en randvillkor.
.
.
Detta ger att , då r = 2R.
Från tidigare så hade vi att , då r = R.
Två villkor och två okända konstanter.
PATENTERAMERA skrev:.
.
Detta ger att , då r = 2R.
Från tidigare så hade vi att , då r = R.
Två villkor och två okända konstanter.
Men dphi/dr*e_r=cphi då r=2R? -e_r=n och E är ju dphi/dr är ju E
Hänger inte med. Vad vill du ha sagt?
PATENTERAMERA skrev:Hänger inte med. Vad vill du ha sagt?
Nej asså jag hänger inte med på vilka villkor du menar. Vi har ju n=-e_r och E=dphi/dr. Sen har jag ju phi(r)=aln(r)+C2 och stoppar man in R så ska det bli lika med phi0. Såhär långt förstår jag. Men sen det här med normalen och E och den där randvillkor förstår jag inte. De kanske menar -dphi/dr*e_r=cphi=E=gradphi. Min gissning är gradphi(2R)=n*E =cphi.
PATENTERAMERA skrev:.
Ja ok jag är med på vad du gör nu.
Då har vi ekvationssystemet
1) phi(r)=aln(r)+C2
2) dphi/dr(r)=cphi(r)
Det första skall du utvärdera då r = R och utnyttja att phi(R) = phi0.
Det andra skall du utvärdera då r = 2R. Tänk på att d(phi)/dr = a/r.
PATENTERAMERA skrev:Det första skall du utvärdera då r = R och utnyttja att phi(R) = phi0.
Det andra skall du utvärdera då r = 2R. Tänk på att d(phi)/dr = a/r.
Ok så om dphi/dr=a/r så implicerar detta att a/r=cphi(r) och stoppar man in r=2R så har vi då a/2R*c=phi(2R)
Då har vi följande ekvationssystem
phi_0=C1ln(R)+C2
C1/2R*c=phi(2R)
Härifrån kan man lösa ut C1
, .
(1).
(2).
PATENTERAMERA skrev:, .
(1).
(2).
Ekvation (2) förstår jag mig inte på eller jag ser inte sambandet. Från ingenstans har det även dykt upp en konstant b som jag inte ser framför mig.
c1 = a. c2 = b. Det är för jobbigt att skriva index.
PATENTERAMERA skrev:c1 = a. c2 = b. Det är för jobbigt att skriva index.
Ok nu hänger jag med.


