Bestäm den horisontella komponenten av normalkraften
Hej! Jag kommer inte vidare på denna uppgiften. 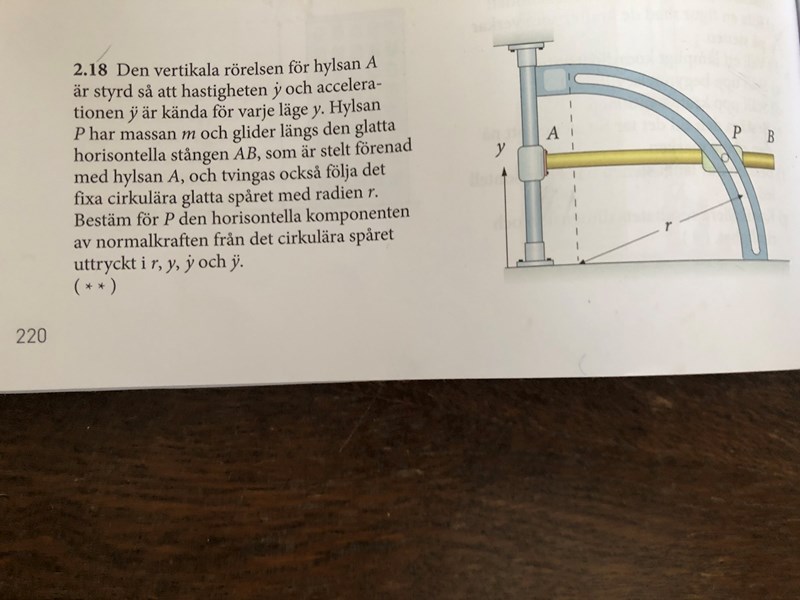
 Min tanke är att använda cylinderkoordinater (ett tvådimensionellt fall, därför är ej z med) för att därefter sätta att ma=F där F är summan av krafterna i samma riktning som accelerationen. Men här har jag stött på patrull.
Min tanke är att använda cylinderkoordinater (ett tvådimensionellt fall, därför är ej z med) för att därefter sätta att ma=F där F är summan av krafterna i samma riktning som accelerationen. Men här har jag stött på patrull.
Är detta fel sätt att lösa denna uppgiften på? Var borde jag tänka annorlunda?
Börja med att uttrycka och derivera sedan fram och .
Tillägg: 10 jan 2024 13:02
Sedan är väl inte riktigt korrekt. Ska väl bara vara egentligen.
Tack för hjälpen. Jag har svårt att tänka vidare med att jag har y men ska uttrycka den horisontella komponenten. Jag tänker att y är den vertikala.
Är det accelerationen i y-led jag har fått fram?
Formeln jag fick fram i y-led är mycket lik formeln för acceleration jag fick fram med cylinderkoordinater.

Så, nu kan du ersätta alla -beroenden i uttrycket för acceleration.
Sedan när du vet objektets acceleration använder du Newtons andra lag för att bestämma krafterna. Fundera då på om din friläggning är helt korrekt.
Tips
Utan det cirkulära spåret, hur skulle friläggningen se ut då?
Tillägg: 10 jan 2024 20:29
Glömde säga att du missat inre derivatan på första termen för .
Aorta skrev:Jag tänker att y är den vertikala.
Ja, men på grund av tvånget för hylsan P längs med det cirkulära spåret resulterar detta i en total acceleration för P som både är vertikal och horisontell. Den hålls i denna bana på grund av normalkraften från spåret.
Är det accelerationen i y-led jag har fått fram?
Japp.
Formeln jag fick fram i y-led är mycket lik formeln för acceleration jag fick fram med cylinderkoordinater.
Ja, det ska den vara eftersom du uttryckt som en transformation från polär till rektangulär koordinat.
Jag tänker att utan det cirkulära spåret hade den inte haft någon normalkraft. Då hade den enda kraften varit gravitationskonstanten. Stämmer det?
När jag försöker tänka om ang min friläggning funderar jag på om det kan vara så att normalkraften i min friläggning är felriktad och att den ska ha samma riktning som enhesvektorn i radiell riktning istället, men det känns inte heller helt rätt då jag tycker att normalkraften brukar "skjuta från" underlaget.
Aha! Jag hade glömt att tänka på att p sitter på en stång! Normalkraften borde då vara vinklad rakt upp tänker jag, motriktad gravitationen.
 Jag försöker lösa ut täta men får problem med den sista. Jag får ett svar med arcsin vilket inte känns korrekt.
Jag försöker lösa ut täta men får problem med den sista. Jag får ett svar med arcsin vilket inte känns korrekt.
Så, tänk på de tre situationerna:
- Inget cirkulärt spår - Normalkraft rakt upp från stången.
- Bara cirkulärt spår och konstant fart - Normalkraft riktad i negativ radiell riktning.
- Med både stång och spår - ???
Tänk på att en kraft leder till en acceleration. Du vet att hylsan kommer röra sig upp till vänster. Således måste accelerationen vara riktad, medelmässigt, upp till vänster.
Jag är med på resonemanget ang normalkraften tror jag. Men jag tänker att normalkraften med både stång och spår borde bli riktad snett upp mot höger då de två komponenterna till normalkraften adderas.
SaintVenant skrev:Så, nu kan du ersätta alla -beroenden i uttrycket för acceleration.
Jag förstår inte hur jag ska ersätta θ. När jag försöker lösa ut θ får jag inte bort cosθ.
Appropå krafterna så har du att normalkraften från spåret omöjligt kan vara riktat upp till höger. Detta därför att det skulle innebära en acceleration till höger. Hylsans rörelse i spåret kommer inte vara något till höger. Du kanske blandar ihop centripetal- och centrifugalkraft?
Tänk på att du i detta fall inte fixerar ett koordinatsystem i hylsan utan i ett inertialt referenssystem. Då är rörelsen totalt sekanten upp till vänster. Accelerationen måste således ha en komponent åt vänster.


