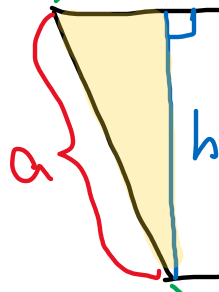
Bestäm den minsta möjliga omkrets parallellogrammen kan ha, om dess area är 77 cm^2 (A)

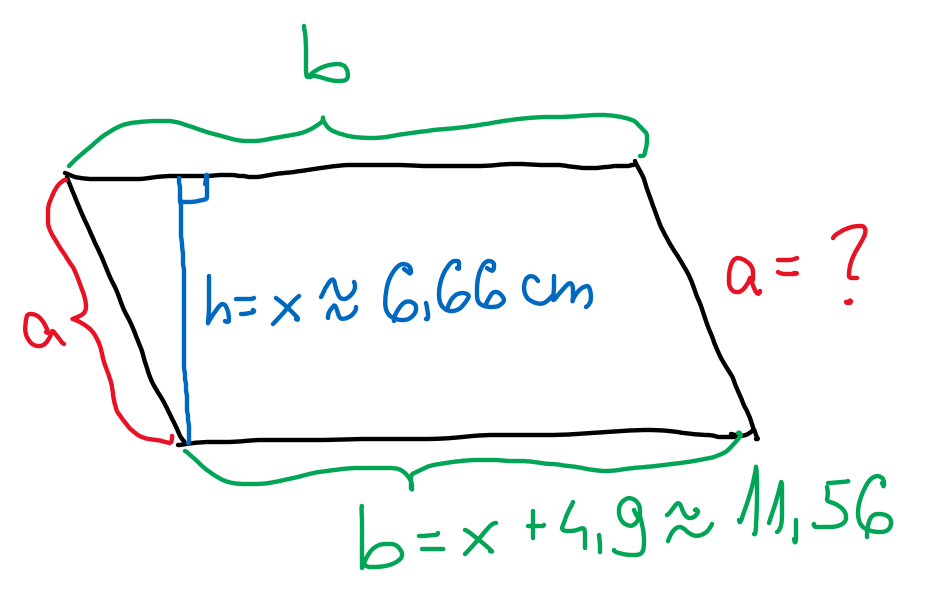
Du har beräknat att höjden är lika med (cirka) 6,66 cm, så basen är lika med (cirka) 11,56 cm.

Omkretsen innehåller dock också de sneda sidorna, d.v.s. omkrets = 2a+2b enligt figuren nedan. Vad är det minsta möjliga värdet på a?

Om vi kallar den lutande sidan för a och vinkeln mellan sidan a och basen b för f får vi följande samband

1:  h = a*sin(f)

Dessutom vet vi att 

2:  h+4,9 = b

Omkretsen, O, är 

3:  O = 2a+2b som vi ska hitta minimum för

Ture skrev:

 

Om vi kallar den lutande sidan för a och vinkeln mellan sidan a och basen b för f får vi följande samband

1:  h = a*sin(f)

Dessutom vet vi att 

2:  h+4,9 = b

Omkretsen, O, är 

3:  O = 2a+2b som vi ska hitta minimum för

Hmm.. har inte lärt mig det där med sin.

tänkte att jag kanske kunde använd Pythagoras sats men måste ju veta längden på andra katetern. 

och förstår fortfarande inte vad grafen försöker säga. 

maratmatorkin skrev:

...

och förstår fortfarande inte vad grafen försöker säga. 

Vilken graf menar du?

Om sidan a verkligen är lutande, så har man en rätvinklig triangel, där en av kateterna har längden $h\approx 6.66 \text{ cm}$ och hypotenusan har längden $a$. (Den andra kateten är okänd.)

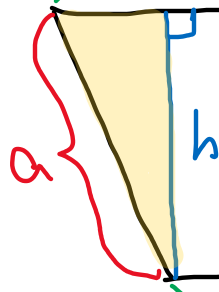
Vilken av sidorna i en rätvinklig triangel är längst?

Kan man då dra någon slutsats om det minsta möjliga värdet på $a$?

LuMa07 skrev:

maratmatorkin skrev:

...

och förstår fortfarande inte vad grafen försöker säga. 

Vilken graf menar du?

---

Om sidan a verkligen är lutande, så har man en rätvinklig triangel, där en av kateterna har längden $h\approx 6.66 \text{ cm}$ och hypotenusan har längden $a$. (Den andra kateten är okänd.)

Vilken av sidorna i en rätvinklig triangel är längst?

Kan man då dra någon slutsats om det minsta möjliga värdet på $a$?

Jag menar grafen till funktionen som jag ritade upp i Geogebra och klistrade in två bilder på, varav en förstorad.

jag förstår inte riktigt kopplingen till ”minsta värdet”, det är lite det jag frågar om.  Är det lite som att titta på en graf för att se hur man får störst area på en rektangelformad hage? Den nivån förstår jag. Men hajar inte det jag räknat ut. Speciellt inte när jag tittar på funktionens graf i Geogebra.

som svar på din fråga. Hypotenusan är den längsta sidan i en rätvinklig triangel. a är lika med roten ur h i kvadrat + okända katetern i kvadrat. 

Oj. Råkade klarmarkera..

hade en annan ansats men den rann ur sanden.

det här var också intressant. En pythagoreisk taltrippel. Nästan va?

Kunde tydligen avmarkera "klarmarkeringen" men bäste livehjälparen Sten kom till min undsättning.