Bestäm den största sträcka med vilken bilen ligger efter loket

På en lång raksträcka löper en landsväg jämsides med en järnväg. En bil står startberedd på vägen då ett tåg med en konstant hastighet på 60 km/h närmar sig bakifrån.

Just då loket passerar bilen startar denna (vid tiden t=0). Med konstant acceleration når bilen hastigheten 90 km/h på 10 sekunder. Därefter bibehåller bilen denna hastighet.

b) Bestäm den största sträcka med vilken bilen ligger efter loket.

För att lösa denna tänkte jag teckna en funktion som beskriver avståndet mellan bilen och tåget efter tiden t sekunder och därefter hitta maximipunkten. Y - värdet anger den maximala sträckan. Jag gjorde enligt följande:

Sträcka tåg: $(\frac{60}{3, 6}) t$

Sträcka bil (accelerationen beräknade jag till 2,5 m/s^2): $\frac{2, 5 t^{2}}{2} + 25 t$

S(t) = sträcka bil - sträcka tåg : $s (t) = (\frac{2, 5 t^{2}}{2} + 25 t) - \frac{60}{3, 6} t d ä r 0 < t < 20$

Jag skriver in detta i min räknare men får en maximipunkt där t är negativt och dessutom fel maximivärde.

Vad är det jag missar?

(Kom på att i s(t) underlättar det om jag skriver lokets sträcka först)

Uttrycket för bilens sträcka stämmer inte. Du får dela upp det i två fall: om bilen fortfarande accelererar, eller om den har kommit in i fasen med konstant fart.

Fundera på det här:

När bilen står stilla och loket blåser förbi kommer avståndet mellan dem att vara noll.
Bilen accelererar men eftersom tåget håller en högre hastighet kommer avståndet att öka. Det kommer att fortsätta öka tills bilen nått lokets hastighet.
I det ögonblick bilen kommit upp i samma hastighet som loket så slutar avståndet att öka.
I och med att bilen fortsätter accelerera kommer avståndet därefter att minska, eftersom bilen då kör snabbare än loket.

Till slut kommer bilen ikapp loket och kör om, men det vi är intresserad av är #3 ovan.

Du menar att avståndet är som störst fram till att bilens hastighet är lika med lokets hastighet?

Anonym_15 skrev:
Du menar att avståndet är som störst fram till att bilens hastighet är lika med lokets hastighet?

Ja. Avståndet är som störst exakt när bilens och lokets hastigheter är lika stora.

Tänk själv: Tåget håller 60 km/h. Bilen håller 0, 10, 20, 30 ... men eftersom tåget kör snabbare så ökar avståndet hela tiden. Det ökar mindre och mindre, men det ökar. När bilen kommit upp i 60 km/h så kör de lika snabbt. Då slutar avståndet att öka.

Har du någon idé om vad du behöver räkna ut?

Jag tar reda på tiden då bilens hastighet = lokets hastighet = 16,7 m/s. Jag beräknar bilen respektive lokets sträcka efter denna tid. Differensen anger det största avståndet. Kan det stämma?

Men om jag vill använda min metod med en funktion s(t) som anger differensen mellan sträckorna och hitta ett maxvärde. Vad gör jag för fel då?

Anonym_15 skrev:
Jag tar reda på tiden då bilens hastighet = lokets hastighet = 16,7 m/s. Jag beräknar bilen respektive lokets sträcka efter denna tid. Differensen anger det största avståndet. Kan det stämma?

Utmärkt! Det kommer att fungera fint.

Anonym_15 skrev:
Men om jag vill använda min metod med en funktion s(t) som anger differensen mellan sträckorna och hitta ett maxvärde. Vad gör jag för fel då?

Du petade in ett 25t i din beräkning av hur långt bilen hunnit. Den står still när när loket passerar, så i $s = v_{0} t + \frac{a t^{2}}{2}$ är alltså v₀=0.

$s_{l o k} = \frac{60}{3.6} t s_{b i l} = \frac{2, 5 t^{2}}{2} ∆ s = \frac{60}{3.6} t - \frac{2, 5 t^{2}}{2}$

Sedan är det ju bra om du tar lokets sträcka minus bilens, men det insåg du själv.

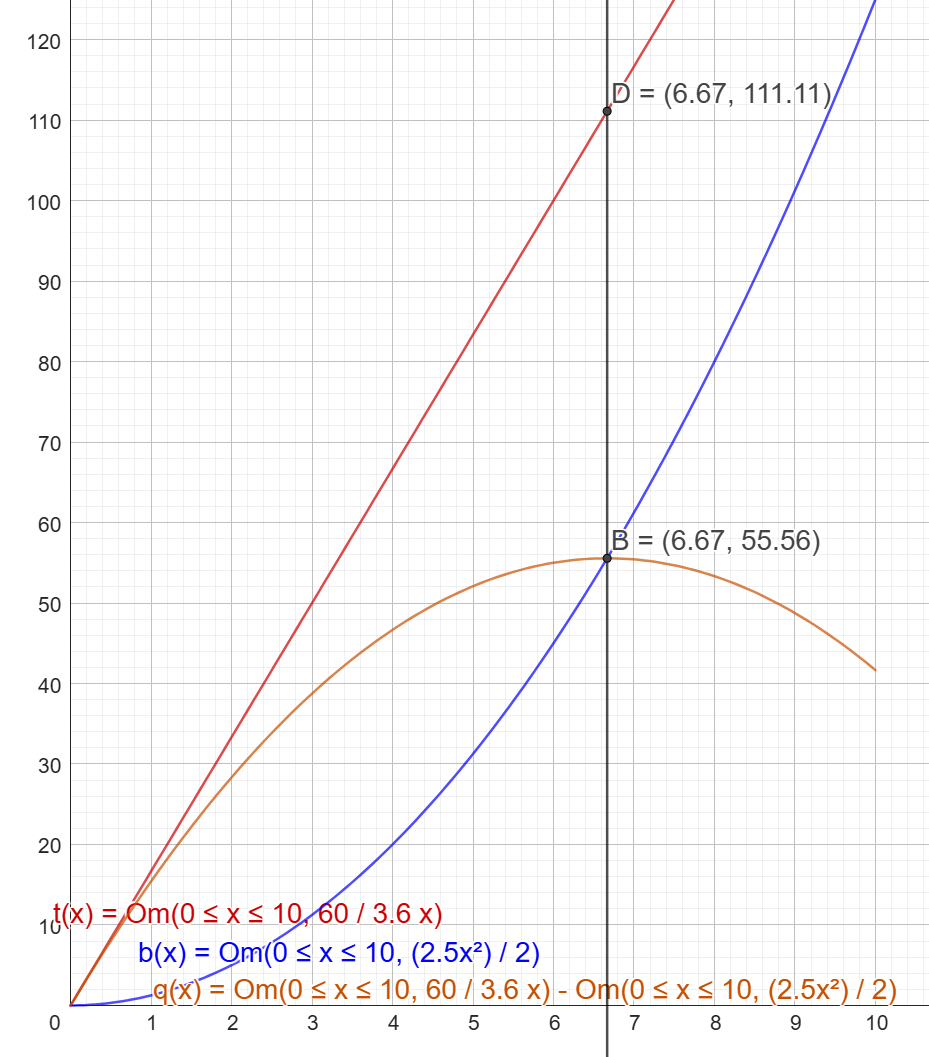
Så här ser det ut. Röd är lok; blå är bil; orange är avståndet mellan dem.

Svara

Visa senaste svar