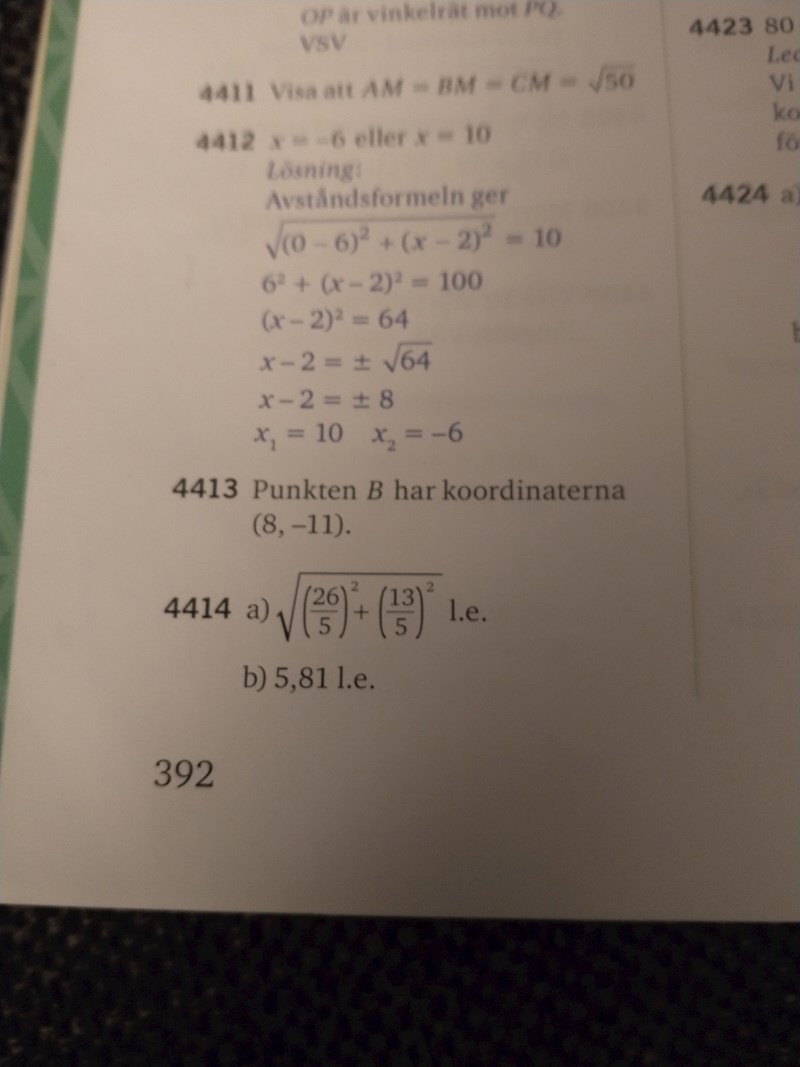Bestäm det kortaste avståndet mellan två linjer
Hej!
Jag kan endast lösa uppgift 4414 här genom trigonometri, men gissar att det finns lättare sätt och att det inte sammanfaller med kapitlets syfte riktigt som är om avståndsformeln.
Så.. hur kan kan göra det? Visar bild på min lösning..
Jag tog punktens värden och stoppade in i linjens ekvation för att få ut X värdet vid Y 2. Det ger en raklinje över som blir hypotenusan i en rätvinklig triangel. Sedan räknade jag fram en godtycklig triangel utifrån linjens ekvation för att kolla dess lutning.
kunde då ta längdenheterna i X (hypotenusan) och ta X cos och sin för vinkeln som är 63.44 för att få ut kateterna på vinkelräta triangeln, varav den längsta kateten då ger kortaste avståndet. 5.81 l.e
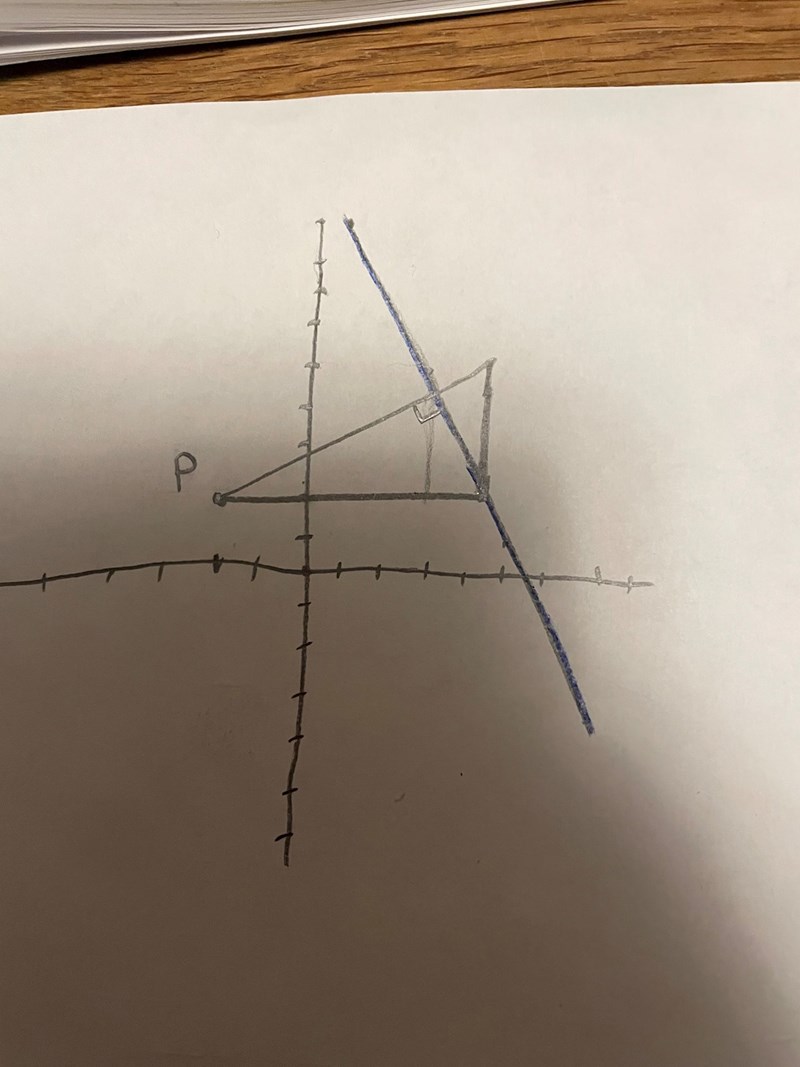

Hej
Du har korrekt ritat att hypotenusan I din triangel skär linjen i rät vinkel.
Detta kan du utnyttja till stt räkna fram ekvationen för den linje som hypotenusan sammanfaller med.
Tänk då på sambandet mellan lutningskoefficienterna för två vinkelräta linjer.
Det blev mer invecklat kanske.
längd enhet för punkten till skärning i X för linjen är 6.5.
Godtyckliga värden för triangeln enligt linjens ekvation ger K = 2.
vi vet att förhållandet måste bli -1. Alltså är K värdet för triangeln jag vill konstruera (eller lutning på kateten) = K 0.5
löngdenhet 6.5*0.5 ger 3.25 i Y.
Vi vet att K för linjen är 2, så vi kan nu ta då 3.25*0.5 för att få skillnaden i Y från skärningspunkten X till skärningspunkten i Y i en liten rätvinklig triangel som är 1.625.
vi får då Y = 3.25-1.625= 1.625.
pluggar in det i första linjens ekvation för att få X värdet vid den här y punkten som blir 4.6875.
Nu har vi två kateter 4.6875 och 1.625.
Med Pythagoras sats blir det 4.961…
Eller nej jag är helt borta någonstans får börja om
Den givna linjen har ekvationen 2x+y = 11, dvs y = -2x+11
Vi letar efter en normal till denna linje (dvs en linje som är vinkelrät mot den), som dessutom går genom punkten (-2, 2).
Normalen har ekvationen y = k2x+m2
Eftersom den första punkten har riktningskorfficirnten 2 så har vi att 2•k2 = -1, dvs k2 = -1/2.
Normalen har alltså ekvationen y = -(1/2)•x+m2.
Vi kan nu bestämma m2 genom att normalen ska gå genom punkten (-2, 2).
Det ger oss att 2 = -(1/2)•2+m2, dvs m2 = 3.
Normalens ekvation är alltså y = -(1/2)•x+3.
Ta nu fram skärningspunkten mellan de två linjerna.
Avståndet mellan dessa två punkter är det som efterfrågas.
Okej.. Jag får att de skär i varandra vid X 5.333 och Y 0.34. Känns inte riktigt rätt
Dkcre skrev:Okej.. Jag får att de skär i varandra vid X 5.333 och Y 0.34. Känns inte riktigt rätt
På a-uppgiften ska du svara exakt, vilket innebär att du behöver ange skärningspunkten (16/3; 1/3) utan att avrunda.
Får fram 5.33 i X sedan 0.34 i Y. Jag vet redan svaret sen min trigonometrilösning och 5.81^2-5.33^ ger då 2.33.
Är helt borta på hur jag ska få Y ~2.33. Antar att 0.34 plussas på 2 värdet av någon anledning
16/3?? :/
Jag tror det blev fel i beräkningen ovanför. k för den ursprungliga linjen är -2, inte 2.
Dkcre skrev:Får fram 5.33 i X sedan 0.34 i Y. Jag vet redan svaret sen min trigonometrilösning och 5.81^2-5.33^ ger då 2.33.
Är helt borta på hur jag ska få Y ~2.33. Antar att 0.34 plussas på 2 värdet av någon anledning
Använd avståndsformeln (Pythagoras sats) för.att beräkna avståndet mellan de två punkterna (-2; 2) och (16/3; 1/3).
Laguna skrev:Jag tror det blev fel i beräkningen ovanför. k för den ursprungliga linjen är -2, inte 2.
Tack Laguna, det stämmer.
Första linjen y = -2x+11 har riktningskoefficienten k1 = -2.
Andra linjen har alltså riktningskoefficienten 1/2, inte -1/2 som jag felaktigt skrev ovan.
Men eftersom jag även satte in x = 2 istället för -2 så gjorde jag ytterligare ett teckenfel som tog ut det andra.
m2 för normalen blir ändå 3:
2 = (1/2)•(-2)+m2
2 = -1+m2
m2 = 3
Jag grejar det inte.
5.33-(-2) är 7.33 och 2-0.34 är 1.66
Der blir 7.52
Dkcre skrev:Jag grejar det inte.
5.33-(-2) är 7.33 och 2-0.34 är 1.66
Der blir 7.52
Men du ska inte använda närmevärden.
Använd det exakta 1/3 istället för 0,34 och 16/3 istället för 5,33.
Läs svar #10 igen.
Okej Yngve, jag skrev det vara för det var lättare att skriva. Men likväl blir beräkningen fel.
Men avståndet mellan dessa punkter i X är (16/3)- (-2) och 2-(1/3). Jag kan inte få ihop det till ~ 5.81
Jag förstår inte riktigt din första uträkning.
Är det den blåmarkerade sträckan som du har längdberäknat till ungefär 5,81 l.e.?
I så fall är det inte detta som efterfrågas.
Istället är det längden av den rödmarkerade sträckan som efterfrågas.
Jag får den till l.e.
Vad står det i facit?
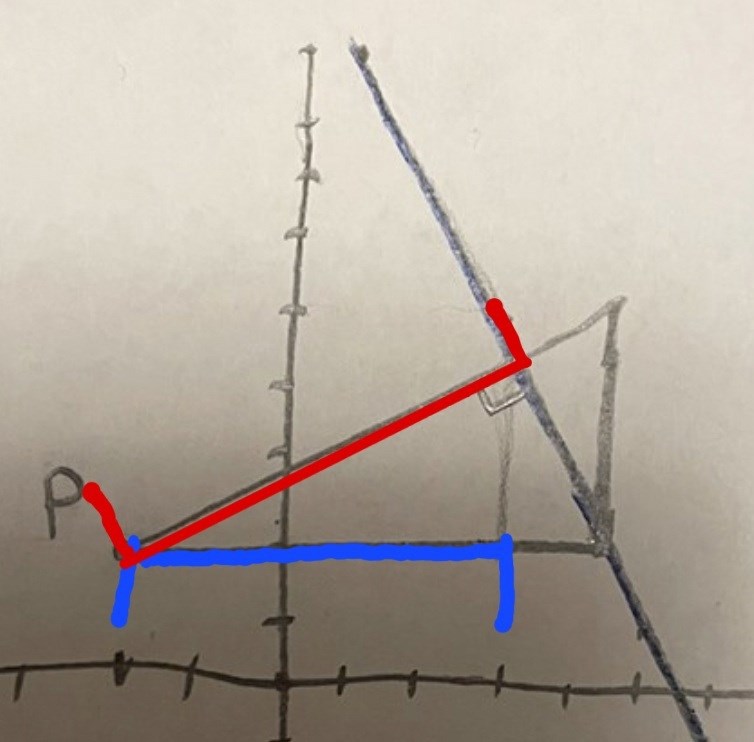
Nej om man drar ut den blåa där ända tills den tangerar linjen. Då har den Längd X6.5 och blir hypotenusan och den röda en katet
Sedan med hjälp av ekvationen vi redan fått för första linjen kan vi bilda en triangel och kolla vinkeln. Exempelvis Y 1 x5 och y2 och X4.5.
Om vi då tar Tan^-1 (1/0.5) får vi vinkeln 26.57.
Vi vet att linjerna är rätvinkliga, och då måste nästa vinkel vara 90-26.57 = 63.44
Sedan tar vi då 6.5*SIN(63.44) =5.81
Har representerat detta med den lilla triangeln där till höger om linjen vi får. Den blir ju likformig med den stora.
Det står a) SQRT((26/5)^2 + (13/5)^2
B) 5.81
Jag är förvirrad.. 😅
Jag får normalens ekvation till y = x/2 + 3 och skärningspunkten till (16/5, 23/5), och det ger det som står i facit.
Ja, jag har räknat fel, ber om ursäkt för det.
Normalens ekvation är
Linjernas skärningspunkt är
Avståndsformeln ger
Hur hittar man linjers skärningspunkt?
0.5X+3 = 11 -2X lär ju vara fel... Eller jaha nej det blir 8/2.5 där ja istället.
Det förklarar saken då
Tack så mycket för hjälpen, hade inte hört om "normalen" och så förut.
Du behöver inte lära dig begreppet "normal".
Det du behöver kunna är att sambandet mellan riktningskoefficienterna k1 och k2 lyder k1•k2 = -1 om linjerna är vinkelräta.