Bestäm det skuggade området som inneslutar 2 funktioner (Matematik/Matte 4/Integraler och tillämpningar)

Så här har jag tänkt

Ni kan kommentera om jag har fått någhra felsteg. Eller om jag kunde ha tigit några "genvägar" för att lösa liknande problem lättare

Integralen som du tecknat, $\displaystyle \int_0^2 (x^2 - 4x + 4)\,dx$ beräknar arean av ett annat område, nämligen det område som avgränsas nedåt av den räta linjen y=4x-4 i hela intervallet 0 < x < 2:

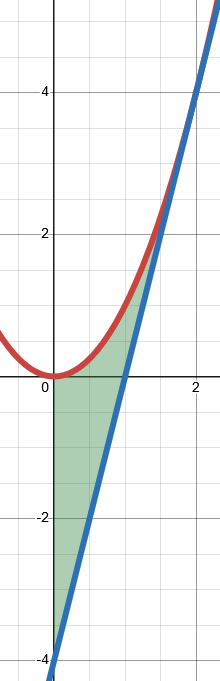
(Ett ytterligare fel uppstod vid beräkningen av F(0) där 3:an i exponenten felaktigt försvunnit och ersatts med 0)

jag förstår men funktionen $y = x^{2} - 4 x + 4$ kan väl skrivas om som $y = {(x - 2)}^{2}$

och sen kan jag väl bara integrera med avseende på $x$ .

Det stämmer att $x^2 - 4x + 4 = (x-2)^2$ och man kan bestämma primitiva funktionen precis på det sätt som du gjort.

Detta är fortfarande fel p.g.a. de problem som jag påpekat i förra inlägget. (Fel område och fel insättning i F(0))

ok, så hur skulle man kunna ställa upp integranden på korrekt sätt ?

Tillägg: 25 jan 2026 13:21

Skulle man kunna dela upp integralerna ?

$\int_{0}^{2} {(x)}^{2} d x - \int_{0}^{2} (4 x - 4) d x$

Arup skrev:
Skulle man kunna dela upp integralerna ?

$\int_{0}^{2} {(x)}^{2} d x - \int_{0}^{2} (4 x - 4) d x$

Det är fortfarande fel område.

Ska området gå nedåt hela vägen till linjen y=4x-4 för alla x mellan 0 och 2?

Nej! Det är en annan linje som avgränsar området nedåt i vänstra delen av intervallet 0<x<2.

ok, så hur ska det bli ?

Området mellan två kurvor bestäms m.h.a. $\displaystyle \int_a^b (\text{övre}\left(x\right) - \text{undre}\left(x\right))\,dx$ , där $a$ och $b$ är $x$ -koordinaterna av vänstra respektive högra ändpunkten.

Betrakta figuren nedan, där det önskade området ritats ut:

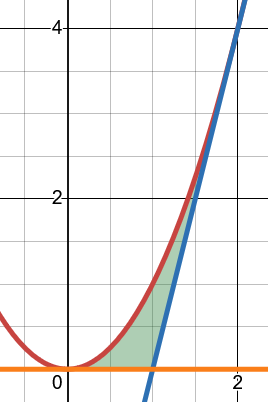
I figuren ser man att parabeln $y=x^2$ är den övre kurvan för alla $x$ mellan $0$ och $2$ .

Det finns dock två olika linjer som blir den undre kurvan beroende på värdet på $x$ .

Vad är ekvationen för den orange linjen?
För vilka $x$ är det just den orange linjen som utgör områdets undre kant?
För vilka $x$ är det den blå linjen $y=4x-4$ som utgör områdets undre kant?

Besvara dessa tre frågor innan vi går vidare.

Den orgea linjen har väl ekvationen $y = 0 ?$
Jag vet inte riktigt vad dun menar här Är det för x mindre än noll =
kan inte jag sätta y=0 för att lösa ut x-koordinaterna ?

Den sökta arean är skillnaden mellan integralen av x² från 0 till 2 som blir 8/3 och den vita triangeln i ``8 ovan.

Den givna funktionen g ger för y=0 att x=1 så triangelns area är 4x1/2=2 Så den sökta arean blir 8/3 - 2 =2/3.

Arup skrev:

Den orgea linjen har väl ekvationen y=0 ?

Jag vet inte riktigt vad dun menar här

Ja, det stämmer att y=0 är ekvationen till den orange linjen.

Tänk dig att området är omslutet av stängsel med tre olika färger - rött, blått och oranget - beroende på vilken kurva som utgör gränsen. Man vill ta reda på x-värdena där man har det blå stängslet respektive det orange stängslet, d.v.s.

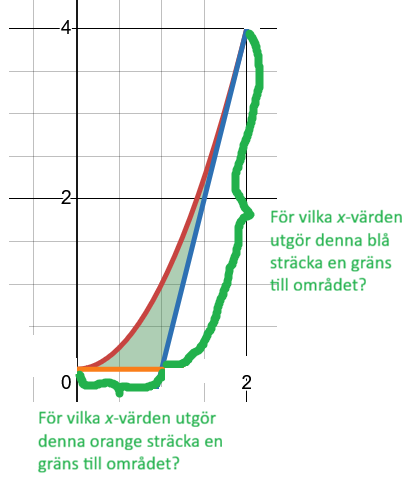
Det går bra att sätta y=0 för att lösa ut x-koordinaterna.

ja men, det här är ju en triangel

Notera att du fått två förslag på lösningar:

LuMa07 i #9: Den röda över x-axeln en bit plus den röda över den blå.
Hansa i #11: Den röda över x-axeln hela vägen minus triangeln som den blå bildar mot x-axeln.

Båda sätten går bra. Det andra är nog enklare.