Bestäm ekvationen för de tangenter till kurvan: 𝑦 = 2𝑥^3 − 3𝑥^2 − 60𝑥 som har k-värdet 12

När du gör -12 på i båda leden råkar du göra +12 i VL

När du fått fram x-värdena, i vilket uttryck hittar du y-värdena för kurvan?

Så det ska alltså vara y'=6x²-6x-72?

Fick att y'₁ är likamed - 40,52 och y'₂ är likamed  -60 när jag satt in de olika x-värdena i y'=6x²-6x-60. Jag antar att det ska finnas två ekvationer som svar, alltså att det finns två tangenter. Nu stämmer ju inte x-värdena, men visst ska jag sätta in dem i den deriverade ekvationen för att sedan få ut y-värden och till sist räkna ut y=kx+m?

Om du sätter in x-värdena i y' så får du förstås 12, om du har räknat rätt. Sätt in dem i y så får du tangeringspunkterna.

McDonken skrev:

Så det ska alltså vara y'=6x²-6x-72?

Du har deriverat rätt med när du sätter det lika med 12 förenklar du fel:

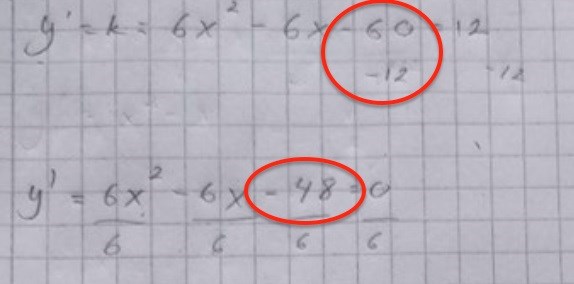
Och som Laguna skrev, för att få fram y ska du sätta in x-värdena i y(x), inte i y'(x). Du vill ju veta tangeringspunkterna för y(x).

Programmeraren skrev:

McDonken skrev:

Så det ska alltså vara y'=6x²-6x-72?

Du har deriverat rätt med när du sätter det lika med 12 förenklar du fel:

Och som Laguna skrev, för att få fram y ska du sätta in x-värdena i y(x), inte i y'(x). Du vill ju veta tangeringspunkterna för y(x).

Hur ska man få fram ekvationen efter man hittade tangeringspunkterna då? 

realone skrev:

Hur ska man få fram ekvationen efter man hittade tangeringspunkterna då? 

En tangent är en rät linje y = kx+m.

Ta en tangent i taget.

Du känner till k-värdet och vill nu bestämma m-värdet.

Om du känner till koordinaterna (x₁, y₁) för en punkt på tangenten så kan du beräkna m-värdet genom att lösa ut m ur ekvationen y₁ = kx₁+m.

Du kan enkelt ta fram koordinaterna för en punkt på respektive tangent.

Laguna skrev:

Om du sätter in x-värdena i y' så får du förstås 12, om du har räknat rätt. Sätt in dem i y så får du tangeringspunkterna.

När jag sätter in x₁ i y`så får jag 12 men när jag sätter in x₂ då får jag en annan svar. Har jag räknat fel eller är det frågan som har bara en svar?

y' ska vara 12, så om det inte blir 12 så har du gjort fel, ja.

Visa hur du löst andragradsekvationen inklusive vilka två x du har fått fram.

.

Programmeraren skrev:

Visa hur du löst andragradsekvationen inklusive vilka två x du har fått fram.

Laguna skrev:

y' ska vara 12, så om det inte blir 12 så har du gjort fel, ja.

 

Blir det svaret då? Ska jag strunta i x₂ då?

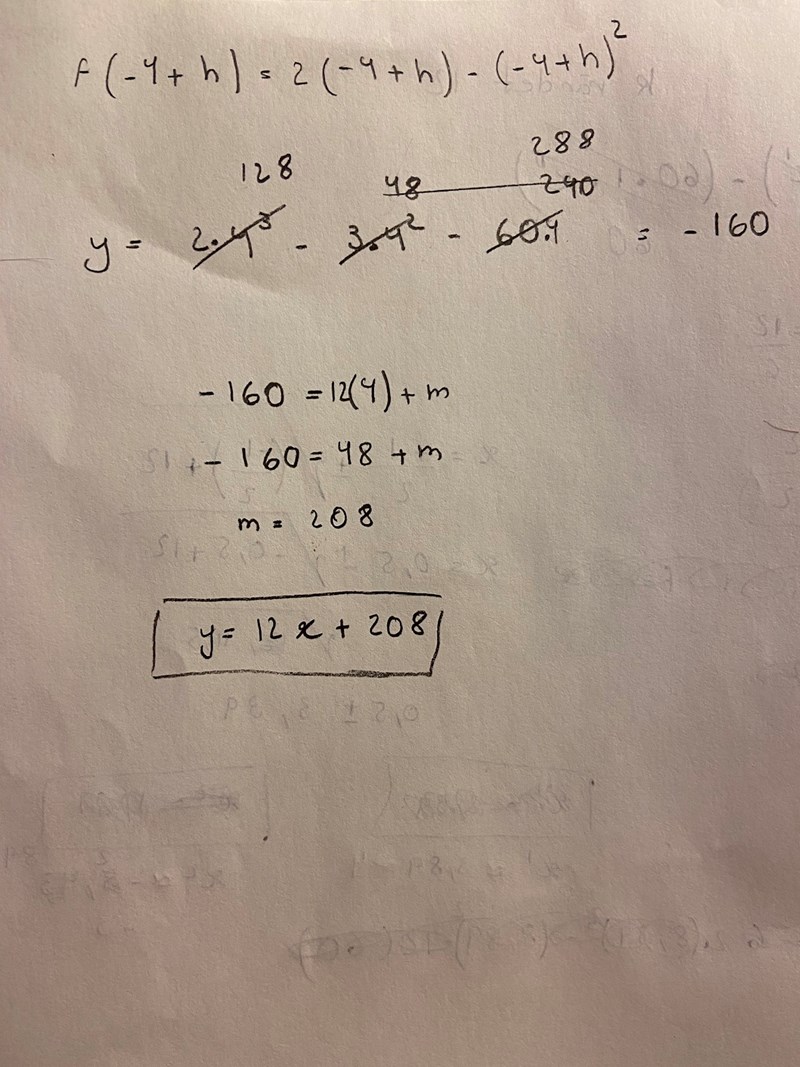
PQ-formeln: Du ska ta "halva koefficienten framför x" i kvadrat under rottecknet.

Programmeraren skrev:

PQ-formeln: Du ska ta "halva koefficienten framför x" i kvadrat under rottecknet.

Så ligger inte i formelbladet. Jag har gjort ett fel och det är att jag har inte multiplicerat 0,5 med sig själv men detta kommer inte alls påverka svaret. Kan du se om jag har fått rätt svar?

Jag visar lösningen av ekvationen, titta igenom så att du är säker på pq-formeln.

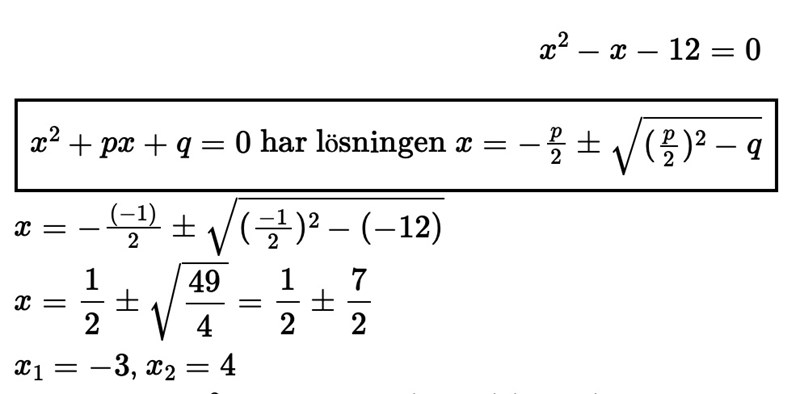
Du vet k-värdet. Du vet de två x-värdena, använd ett i taget. Eftersom du vet x kan du enkelt få fram y.
Då har du det du behöver för att beräkna m i uttrycket:
y=kx+m

Programmeraren skrev:

Jag visar lösningen av ekvationen, titta igenom så att du är säker på pq-formeln.

Du vet k-värdet. Du vet de två x-värdena, använd ett i taget. Eftersom du vet x kan du enkelt få fram y.
Då har du det du behöver för att beräkna m i uttrycket:
y=kx+m

Tack! Braa jag har fått samma svar. kan du kolla på den andra sidan om mitt svar på hela frågan är rätt?

realone skrev:

Programmeraren skrev:

Jag visar lösningen av ekvationen, titta igenom så att du är säker på pq-formeln.

Du vet k-värdet. Du vet de två x-värdena, använd ett i taget. Eftersom du vet x kan du enkelt få fram y.
Då har du det du behöver för att beräkna m i uttrycket:
y=kx+m

Tack! Braa jag har fått samma svar. kan du kolla på den andra sidan om mitt svar på hela frågan är rätt?

 

Dessutom när jag sätter in -3 så får jag inte 12 som k värde. Ska jag strunta i den då? Ska jag bara svara med x₁=4

y'(-3)=12.

Om du inte får det bör du ta reda på varför, troligen gör du något räknefel som det är viktigt att du lär dig åtgärda.
Gissar på att du gör fel på 2*(-3)^3 men visa gärna din uträkning.

y(4)=-160, korrekt

När du sen löser
-160=12*4+m
gör du teckenfel

,

(-3)^2=9 och inte -9
(Även fel i nästa steg, -54+18-60=-96 och inte 96 men som spelar mindre roll eftersom (-3)^2=54)

y'(-3) =
6*(-3)^2-6*(-3)-60 =
6*9-(-18)-60 =
54+18-60 = 12

Ekvationen för att få fram m: Du får fel tecken i svaret:
-160=12*4+m
-160=48+m
-160-48=48-48+m
-208=m
m=-208

,

Det ser rätt ut.

Programmeraren skrev:

Det ser rätt ut.

Så är det svaret eller ska jag forsätta? Frågan är "Bestäm ekvationen för de tangenter till kurvan: 𝑦 = 2𝑥^3 − 3𝑥^2 − 60𝑥 som har k-värdet 12" men jag har fått två ekvationer

Varför tog du bort din uträkning i inlägg #24? Trådarna ska inte "förstöras" eftersom det gör det svårt för andra att följa dem.

"Bestäm ekvationen för de tangenter", "de tangenter" betyder att det är mer än 1. Du ska alltså svara med båda två.