Bestäm en andragradsfunktion med hjälp av högsta höjden och längden mellan "nollpunkten"

Hej och välkommen till Pluggakuten!

Jättebra tänkt. Det känns som om du har bra förståelse och att du bara saknar det där lilla sista.

Det kan du få genom att rita en figur.

Jag skulle föreslå att du först ritar bron som en parabel (ledsen mun) och sedan lägger in ett koordinatsystem med origo i nivå med havsytan och precis under brons högsta punkt.

Då kommer maximipunkten nämligen att hamna precis där du skrev, i (0, 28).

Pröva och visa din skiss.

En sista kommentar är att du bör skriva andragradsfunktionen som $ax^2+bx+c$.

Hej, Tack för snabba hjälpen! så här gjorde jag: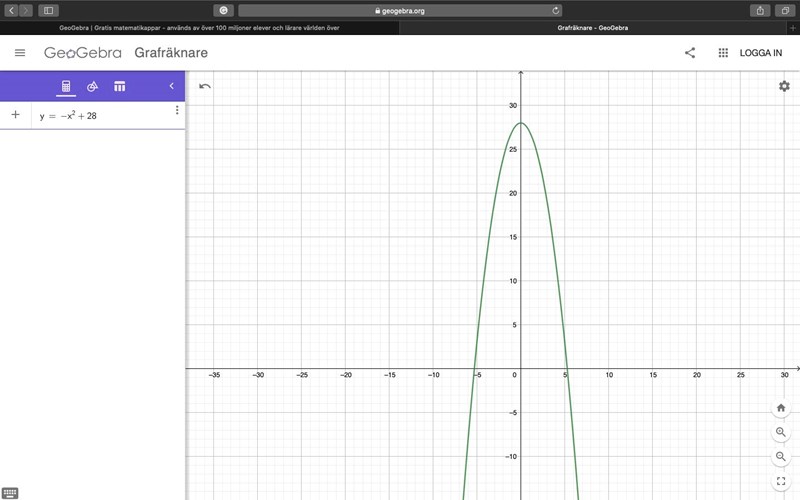

Men längden mellan nu -5 och 5 ska vara 105 meter och jag testade att lägga in de som "q" men då blev mitt y inte 28. jag har fastnat här. eller är det rätt att -5 och 5 är mina nollpunkter och att skriver jag det i en funktion så blir det rätt?

Om $y = ax^2+bx+c$ så bestämmer konstanten $a$ hur pass mycket "skålad" parabeln ska vara.

Nu har du a = -1. Pröva ett annat värde.

Jag inser att det saknas viss information för att kunna lösa uppgiften, nämligen hur högt ovan vattenytan som brofästena befinner sig. Finns det mer information eller kanske någon bild som hör till uppgiften?

Så här ser själva uppgiften ut och jag har bara två tal att jobba med

Tror du att funktionen de letar efter är denna: y=-0,0105x^2+28?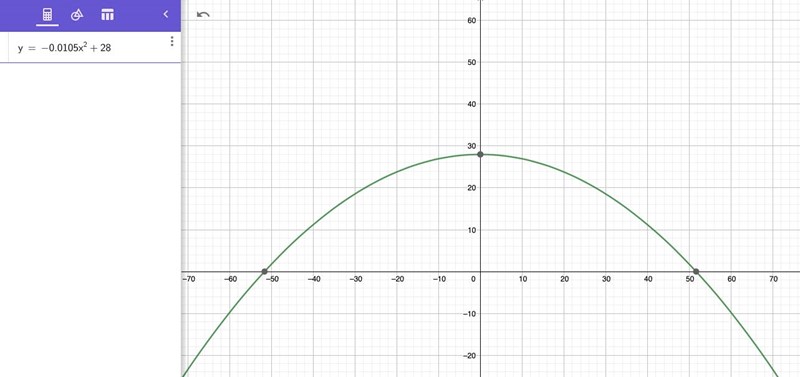

OK då antar vi att brofästena är i nivå med vattenytan, dvs vid y = 0.

Om din funktion är rätt eller inte kan du enkelt kontrollera själv.

Du har tre punkter givna, nämligen (0; 28), (-52,5; 0) och (52,5; 0).

Stämmer de tre punkterna med din funktion?

I så fall har du fått fram rätt funktion, annars inte.

Okey, Tusen tack!!!

Vad kom du fram till?

Stämde dina konstanter med de.tre punkterna?

Är du redo att lära dig hur du kan lösa uppgiften algebraiskt utan att behöva pröva sig fram?

Det var rätt! Ja juste det tänkte jag inte på! vill jätte gärna lära mig det. 

idrottare skrev:

Det var rätt! Ja juste det tänkte jag inte på! vill jätte gärna lära mig det. 

Hmmm, visa då hur du räknade för konstanten -0,0105 är nämligen inte riktigt rätt. Däremot är -0,01016 eller -0,0102 hyfsat bra närmevärden.

---------

För att lösa algebraiskt:

Sambandet $y=ax^2+bx+c$ ska gälla för alla punkter på grafen och alltså även för våra tre givna punkter.

Vi börjar med första punkten (0; 28): Här är $x = 0$ och $y = 28$, vilket innebär att sambandet $28=a\cdot 0^2+b\cdot 0+c$ ska gälla, dvs $c=28$.

Andra punkten (-52,5; 0): Här är $x = -52,5$ och $y = 0$, vilket innebär att sambandet $0=a\cdot (-52,5)^2+b\cdot (-52,5)+28$ ska gälla, dvs $0=2756,25a-52,5b+28$.

Tredje punkten (52,5; 0): Här är $x = 52,5$ och $y = 0$, vilket innebär att sambandet $0=a\cdot 52,5^2+b\cdot 52,5+28$ ska gälla, dvs $0=2756,25a+52,5b+28$.

Du har nu två ekvationer och två obekanta $a$ och $b$. Kommer du vidare själv?

Löste den nu. kontrollerade även allt och det stämde. jag fick fram funktionen y=-0,00508x^2-0,27x+28. tack så jätte mycket för hjälpen! Nu är det solklart hur jag ska göra satt in allt i ett ekvationssystem och räknade ut varje variabel med additionsmetoden. Tack

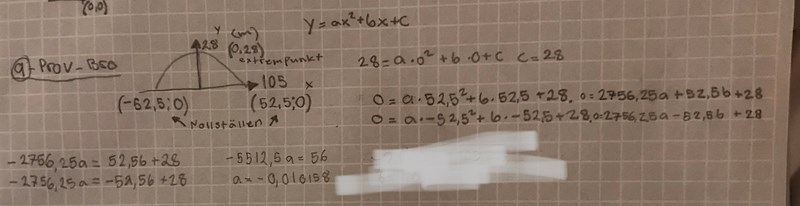Detta är min lösning men jag får a till -0,010158 och vet ej hur jag ska få ut b? 

Houda skrev:

Detta är min lösning men jag får a till -0,010158 och vet ej hur jag ska få ut b? 

Du kommer att få snabbare och bättre svar om du skapar en egen tråd med frågan och där visar hur långt du har kommit.