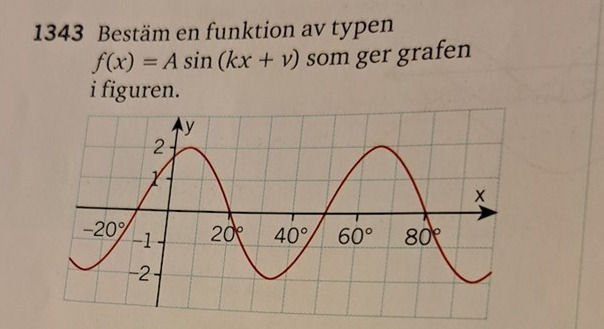
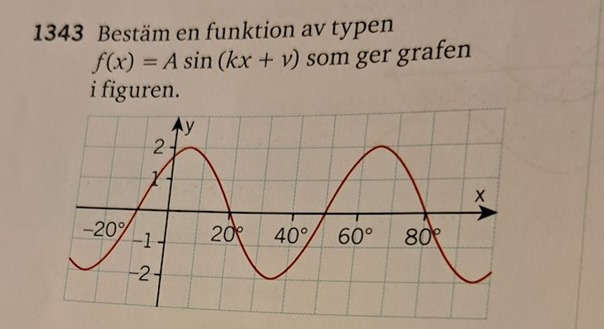
Bestäm en funktion av typen f(x)=Asin(kx+v)
Hej!
I uppgift 1343 så har jag hittat amplituden. Det jag har svårt att nu hitta är förskjutning i x-led ur grafen samt k. Hur gör jag step by step så att jag kan använda denna metod hela tiden på såna frågor? Tar tacksamt emot tips och vägledning!
destiny99 skrev:Hej!
I uppgift 1343 så har jag hittat amplituden. Det jag har svårt att nu hitta är förskjutning i x-led ur grafen samt k. Hur gör jag step by step så att jag kan använda denna metod hela tiden på såna frågor? Tar tacksamt emot tips och vägledning!
Det står i uppgiften att man skall skriva funktionen som en sinusfunktion. En "vanlig", icke förskjuten sinuskurva har y-värdet 0 och positiv derivata när x = 0. För vilket x-värde ser den här kurvan ut på dte sättet?
Smaragdalena skrev:destiny99 skrev:Hej!
I uppgift 1343 så har jag hittat amplituden. Det jag har svårt att nu hitta är förskjutning i x-led ur grafen samt k. Hur gör jag step by step så att jag kan använda denna metod hela tiden på såna frågor? Tar tacksamt emot tips och vägledning!
Det står i uppgiften att man skall skriva funktionen som en sinusfunktion. En "vanlig", icke förskjuten sinuskurva har y-värdet 0 och positiv derivata när x = 0. För vilket x-värde ser den här kurvan ut på dte sättet?
Ah ok. Jag ser att x=20 grader ger y=0 enligt grafen. Jag syftar förresten på uppgift 1343 och ej 1342
Ah ok. Jag ser att x=20 grader ger y=0 enligt grafen.
Nästn - det stämmer att funkntionsvärdet är 0, men viket värde har derivatan?
Jag syftar förresten på uppgift 1343 och ej 1342
Jag tog bort uppgift 1342 när jag kopierade ditt förstainlägg just för att undvika misstag.
Smaragdalena skrev:Ah ok. Jag ser att x=20 grader ger y=0 enligt grafen.
Nästn - det stämmer att funkntionsvärdet är 0, men viket värde har derivatan?
Jag syftar förresten på uppgift 1343 och ej 1342
Jag tog bort uppgift 1342 när jag kopierade ditt förstainlägg just för att undvika misstag.
Vilken derivata och derivatan av vilken funktion? Uppgiften har inget med derivatan att göra som jag förstår,så jag vet ej varför vi blandar in derivata i detta. Hur som helst, vi ser att grafens topp ger oss f'(0)=2
Jaha ok.
Säg lutningen, då! Det skall vara "uppförsbacke" för funktionen när man går åt höger. Eftersom du läser Ma4 trodde jag att det var ett naturligt sätt att uttrycka att funktionen skall vara växnde i en viss punkt.
Smaragdalena skrev:Säg lutningen, då! Det skall vara "uppförsbacke" för funktionen när man går åt höger. Eftersom du läser Ma4 trodde jag att det var ett naturligt sätt att uttrycka att funktionen skall vara växnde i en viss punkt.
Okej men vi har ej kommit till derivata än i kursen. Finns det något annat sätt man kan lösa uppgiften på? Jag lyckades som sagt hitta amplituden.
Vi ser att funktionen har amplitud 2 och period 60 (grader). Värdet på k blir då 360/60 = 6.
Så funktionen är på formen 2sin(6x + v).
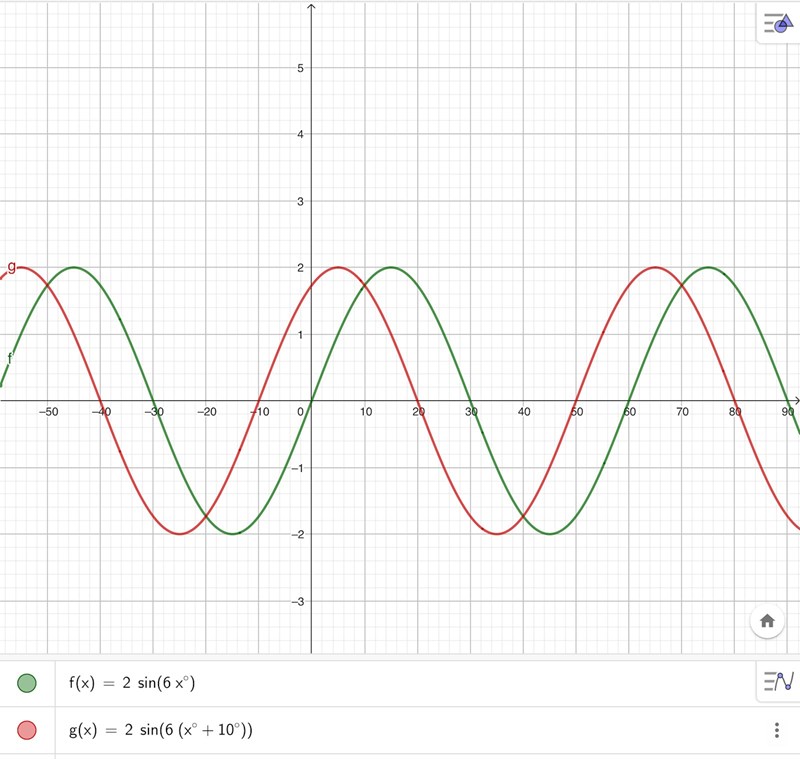
Vi ritar in 2sin(6x) i diagrammet och jämför med den givna funktionen - se nedan. Vi ser att vår funktion är förskjuten 10˚ åt vänster jämfört med 2sin(6x). Vår funktion är därför 2sin(6(x+10)) = 2sin(6x + 60).
destiny99 skrev:Smaragdalena skrev:Säg lutningen, då! Det skall vara "uppförsbacke" för funktionen när man går åt höger. Eftersom du läser Ma4 trodde jag att det var ett naturligt sätt att uttrycka att funktionen skall vara växnde i en viss punkt.
Okej men vi har ej kommit till derivata än i kursen. Finns det något annat sätt man kan lösa uppgiften på? Jag lyckades som sagt hitta amplituden.
Derivata lär man sig i Ma3, så det förväntas su kunna när du läser Ma4.
Leta upp den punkt på kurvan som har y-värdet 0 och där lutningen är positiv. Vilket x-värde gäller det för?
PATENTERAMERA skrev:Vi ser att funktionen har amplitud 2 och period 60 (grader). Värdet på k blir då 360/60 = 6.
Så funktionen är på formen 2sin(6x + v).
Vi ritar in 2sin(6x) i diagrammet och jämför med den givna funktionen - se nedan. Vi ser att vår funktion är förskjuten 10˚ åt vänster jämfört med 2sin(6x). Vår funktion är därför 2sin(6(x+10)) = 2sin(6x + 60).
Det jag tycker är svårt som du gjorde åt mig här är hur jag ska hitta k ur grafen och förskjutningen i x led. Vilken metod använder du och hur ska jag själv på grafen avsläsa perioden,k och v?
k = 360/perioden. Perioden ser du ju direkt i diagrammet. Funktionen upprepar sig efter 60 grader.
Tillägg: 28 jan 2024 16:13
PATENTERAMERA skrev:k = 360/perioden. Perioden ser du ju direkt i diagrammet. Funktionen upprepar sig efter 60 grader.
Tillägg: 28 jan 2024 16:13
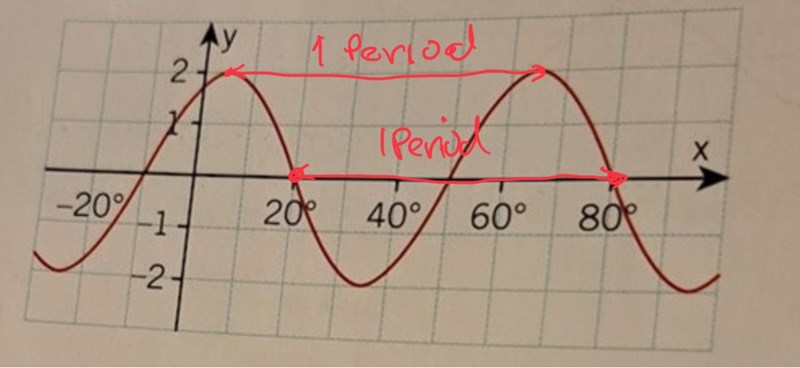
Nej jag ser ej vad perioden är exakt i diagrammet. Var menar du är 60 grader? Det är period ja från ena topp till andra topp. Varför är det en period från en dal till andra dal som ej syns?
En annan sak jag undrar över är hur man ser förskjutningen med vinkel i x-led?
Det är tex 60 graders skillnad mellan två toppar eller mellan två nollställen där derivatan är den samma.
Tex har du en topp för x = 5 och nästa topp då x = 65. 65 - 5 = 60.
Funktionen har tex ett nollställe med negativ derivata då x = 20. Nästa nollställe med negativ derivata är x = 80. 80 - 20 = 60.
PATENTERAMERA skrev:Det är tex 60 graders skillnad mellan två toppar eller mellan två nollställen där derivatan är den samma.
Tex har du en topp för x = 5 och nästa topp då x = 65. 65 - 5 = 60.
Funktionen har tex ett nollställe med negativ derivata då x = 20. Nästa nollställe med negativ derivata är x = 80. 80 - 20 = 60.
Ah okej men då är jag med. Tack!