Bestäm en funktion som uppfyller villkoren
Hej, jag har följande uppgift:
Figuren visar grafen till en andragradsfunktion f.
a) Bestäm en funktion g, där y=g(x), som uppfyller villkoren
- grafen till g är en rät linje,
- g(x) ≤ f(x) för 0 ≤ x ≤ 2
b)Bestäm ekvationen för en rät linje som varken skär grafen till funktionen f eller grafen till funktionen g för något värde på x.
Jag är väldigt osäker hur jag ska tänka här. Nån som kan hjälpa?
Det första villkoret betyder att den kan uttryckas y=kx+m.
Det andra villkoret betyder att den inte får skära det blå området:
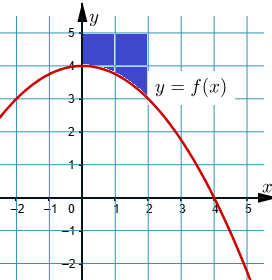
(det blå området fortsätter oändligt uppåt)
När du sen kommer till b-uppgiften så får du skära det blå området med den tredje funktionen.
Varför betyder det andra villkoret att den inte får skära i det blåa området?
Om den skär t.ex. punkten (2, 5), då är g(2) = 5, men f(2) = 3. g(x) får inte vara större än f(x) i intervallet 0-2.
Så för a uppgiften får funktionen vara vad som helst så länge g(x) är mindre än/lika med f(x) i det intervallet? That's it?
Så länge den även är rät, ja =) det finns oändligt många rätta svar.
Okej, så om vi säger att g(x)=x-1
för b uppgiften, innebär det inte bara att den nya räta linjen behöver ha ett m-värde stort nog att inte skära f(x) (typ >5 då) och k-värde1?
Tänk noga på vad den ska ha för k-värde. Det finns bara ett rätt svar, baserat på vad du väljer för k i a). Kom ihåg att h(x) varken ska skära f(x) eller g(x).
Juste, sant, g och h måste vara parallella, både k måste vara samma. Men m värdet kan vara vad som helst annars? så länge det inte når f(x)?
Precis =)
Yes, jag förstår. Tack för hjälpen!



