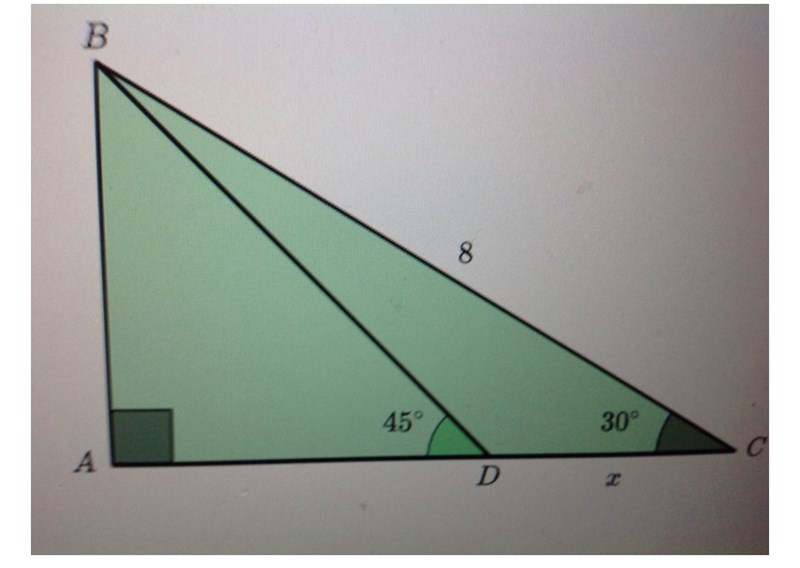
Bestäm ett uttryck

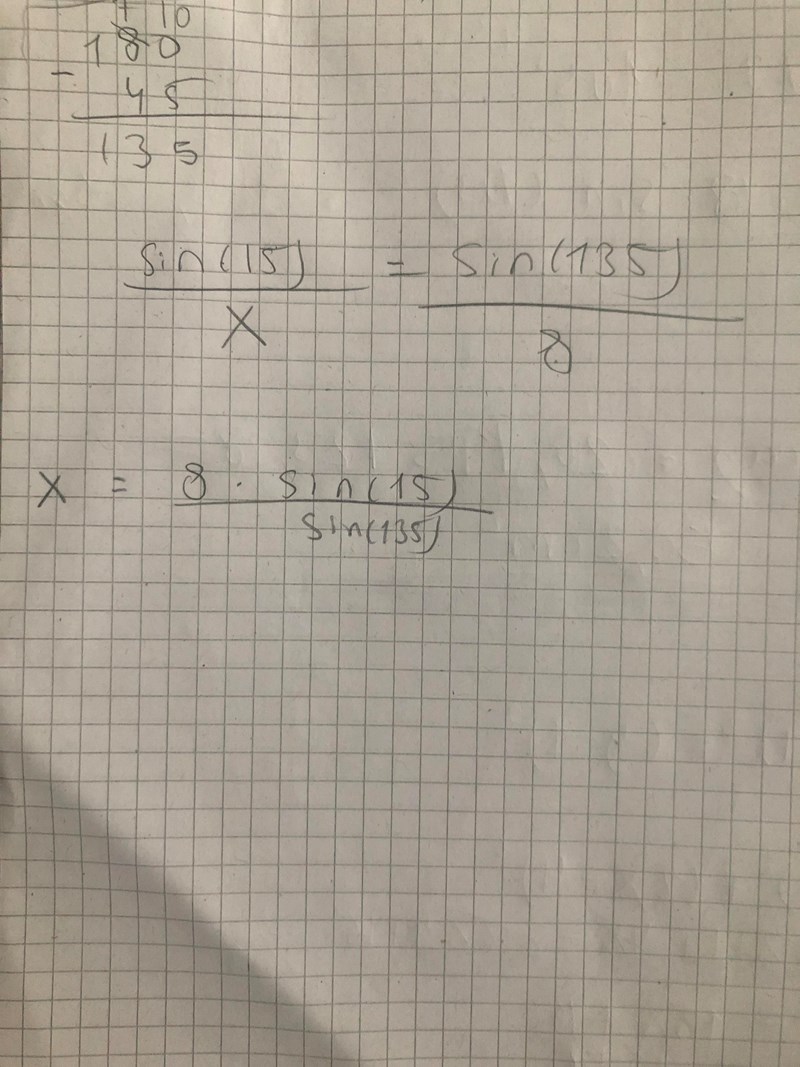
Ebbask skrev:

bestäm ett uttryck för x utan att använda räknare. Svara exakt.

Är min uträkning korrekt

Du har inte löst uppgiften, och du har inte förklarat hur du har tänkt så tydligt att jag kan hänga med.

Som jag fattar det har du:
1.  Räknat ut de övriga vinklarna i triangeln längst till höger
2. Använt sinussatsen för att räkna ut x

Så långt är allt rätt. Men nu skall du svara exakt.

Har ni lärt er formler för summ/differans för sinus? 
$\sin (x\pm y)=\sin \left(x\right)\cos \left(x\right)\pm \cos \left(x\right)\sin \left(y\right)$

Då kan du komma mycket längre. 

Nej vi har inte lärt oss formlerna . Hur ska jag svara exakt

Jag har först beräknat vinkeln vid D genom att ta 180-45=135 grader. 
Därefter har jag beräknat vinkeln B för vinkelsumman är 180 grader.  Mha sinussatsen har jag ställt upp ett uttryck för x

Utnyttja att triangeln ABC är "en halv liksidig triangel" och att triangeln ABD är "en halv kvadrat". 

Okej. Ny lösning.

Vet du att sin(30)=1/2?   Om du inte vet det fungerar inte denna lösning.

Vi vet att
(1)    sin(30)=1/2    
(2)    sin(30)=AB/8           (motstående/hypotenusan)

Detta ger att AB=4

Vidare vet vi att AD=AB    (för att det är en 45,45,90 triangel)

Nu kan vi använda pythagoras sats på triangeln ABC.   Visa ditt försök.

Om AB=4

då är AD=4

x kan beräknas mha Pythagoras sats

(4+x)^2+4^2=8^2

x~ -4+sqrt(3) 

Är det rätt?

Du har inte visat dina beräkningar så ingen kan se vad du gjort och därmed kan ingen hjälpa dig.

Du har fått ett negativt x, är det rimligt?

Ebbask skrev:

Om AB=4

då är AD=4

x kan beräknas mha Pythagoras sats

(4+x)^2+4^2=8^2

Hit ser det rätt ut

x~ -4+sqrt(3) 

Är det rätt?

Här vet jag inte alls hur du har räknat, men ett negativt värde på en sträcka tyder på att något är fel.

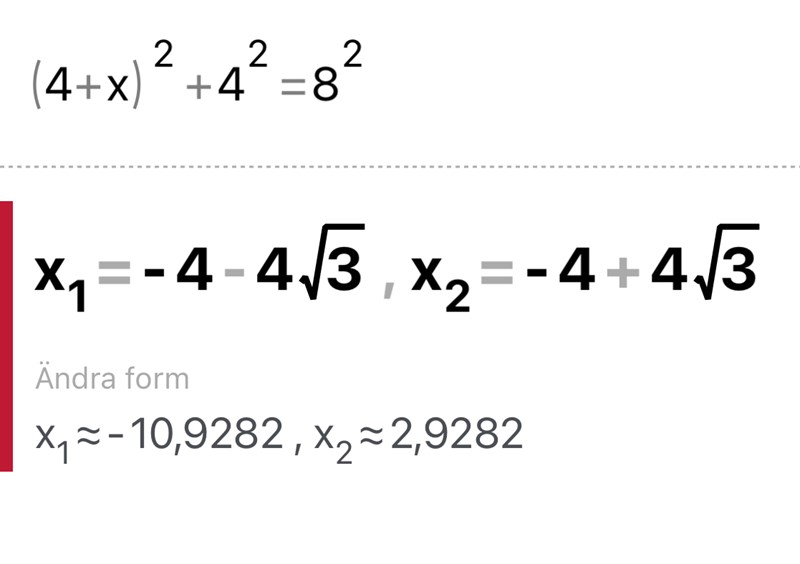Negativ x utesluts då det inte kan finnas negativa längder. X2 är ju inte negativ 

Den här andragradsekvationen måste du kunna lösa för hand. Visa steg för steg hur du gör det.

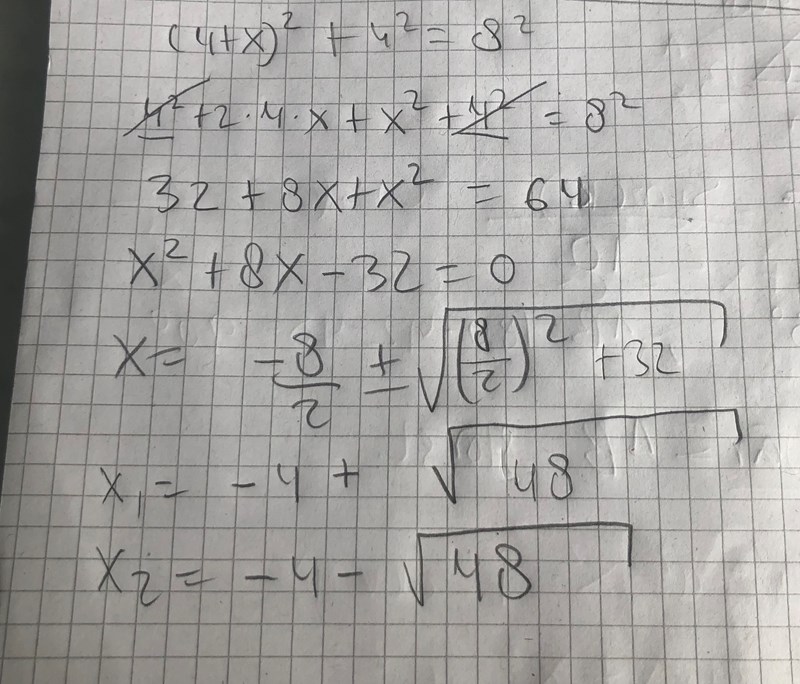Så här gör jag mha PQ formeln 

Är svaret rätt? Dvs x1? Det borde ju vara rätt för x1 är inget negativt tal 

Du hade själv kunnat stoppa in ekvationen i WolframAlpha och kollat om det stämmer.

Ja mitt svar stämmer däremot utesluter jag x2 som ger ett negativt tal