Bestäm Funktionen
Hejsan!
Har råkat ut för en uppgift jag inte riktigt förstår eller vet vart jag skall börja någonstans.
För en funktion f(x)=x2 + bx + c gäller att f(-1)=f(2).
Funktionens minsta värde är -1,25. Bestäm funktionen.
Jag ser på funktionen att x2 är positiv och att parabelns minimipunkt ligger på -1,25
skulle någon kunna förklara vad f(-1)=f(2) betyder?
Är tanken att jag skall lösa ut bx samt c med hjälp av detta?
Välkommen till pluggakuten. f(-1)=f(2) betyder att om du sätter in x=-1 i f(x) och sätter in x=2 i f(x) och sätter uttrycken lika. För att lösa ut b och c.
Hej.
För att lösa den här uppgiften kan du utnyttja att grafen till en andragradsfunktion kallas parabel och att den parabeln har en symmetrilinje.
Parabeln är symmetrisk med avseende på symmetrilinjen, vilket betyder att parabeln ser likadan ut till vänster om som till höger om symmetrilinjen.
Det betyder i sin tur att vertex (i det här fallet minimipunkten) ligger på symmetrilinjen.
Det ger dig en ledtråd till att fundera ut vid vilket x-värde som symmetrilinjen befinner sig, vilket ger dig ytterligare ett samband mellan b och c.
Kommer du vidare då?
--------------
Tips: Rita gärna en figur.
Du kan för resonemangets skull sätta f(-1) = f(2) = 2. Markera dessa punkter och fundera på hur parabeln måste se ut på ett ungefär. Markera symmetrilinjen som ska gå genom parabeln vid y = -1,25.
-----------------
Om dessa begrepp känns obekanta så kan du läsa det här avsnittet. Symmetrilinjen beskrivs på slutet.
Först tänkte jag att det inte går att hitta EN enda funktion när vi bara vet att f(-1)=f(2) men sedan såg jag att det inte fanns något a i uttrycket för f(x) (utan man vet att det är en "osynlig etta"), och då går det!
Jag har suttit och funderat ett bra tag och försökt med olika lösningar.
Jag har kommit fram till att f(-1)=f(2) ser ut såhär.
f(-1) = (-1)2 + b(-1) 1-b+c
f(2) = 22 + b(2) + c 4 + 2b + c
f(-1)=f(2) 1 -b +c = 4 +2b +c
=> 1 -b = 4 +2b
=> -3 -b = 2b
=> -3 = 3b
=> -1 = b
Nu har jag fått ut vad b är och får att f(x) = x2 -x +c.
men det jag fastnar på är hur jag ska få ut vad C är då c tar ut varandra. Jag har funderat på om man kan använda sig utav additionsmetoden för att utesluta vad c är men såg att detta används i linjära ekvationssytem.
Jag har försökt klura ut om jag kan använda mig utav symmetrilinjens (minimipunkten) -1,25 men då jag inte använt mig av dessa metoder tidigare har jag slut på idéer.
Skulle behöva yttligare några råd. Tack på förhand!
Har du läst och förstått allt som Yngve skrev?
Din uträkning är rätt.
Med hjälp av sambandet f(-1) = f(2) kan du komma fram till att b = -1, men du kan inte bestämma c.
Däremot stämmer det att du kan använda symmetrilinjen för att bestämma c.
Du vet att minimipunkten har y-koordinaten -1,25 och att den ligger på symmetrilinjen.
Om symmetrilinjen t.ex. ligger vid så gäller det att , vilket ger dig en ekvation för att bestämma
Du behöver nu ta reda på vad är, dvs vad symmetrilinjen har för x-koordinat.
För att ta reda på det:
- Läs det avsnitt som jag länkade till tidigare och fråga här om det du inte förstår av det som står där.
- Rita den figur jag tipsade om och visa den här.
Om du ändå inte kommer vidare med hjälp av det så finns det en lite krångligare väg att hitta symmetrilinjen.
Klicka här för den krångligare vägen
Symmetrilinjen ligger mitt emellan funktionens nollställen, vilka du kan hitta genom kvadratkomplettering eller med hjälp av pq-formeln.Alternativt:
...
(Verkar som mitt inlägg försvann så ursäktar för sent svar)
Tack! Har gått igenom det du länkade och förstår det mesta.
Det jag inte riktigt är med på är hur jag bestämmer vad c är genom att använda mig utan symmetrilinjens y-koordinat -1,25.
Du nämnde att om symmetrilinjen t.ex.ligger vid x=x0 så gäller det att f(x0)= -1,25 vilket förvirrar mig lite.
Har inte alls jobbat med detta så mycket så ursäkta om jag inte är helt med.
Jag använde mig däremot av pq-formeln för att bestämma symmetrilinjens x-koordinat då jag bestämt vad b är.
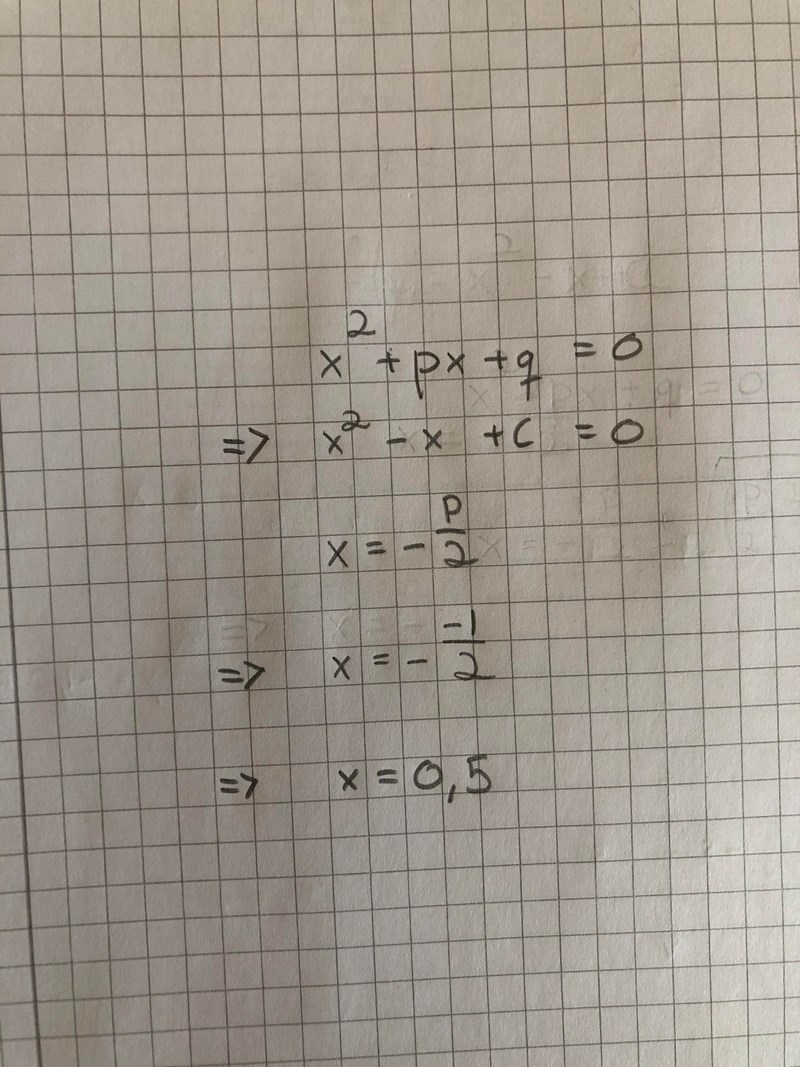
Snyggt. Rätt räknat och bra figur.
Du vet nu att minimipunkten har koordinaterna (0,5; -1,25). Eftersom den punkten ligger på parabeln så måste dess koordinater uppfylla sambandet . Det ger dig en ekvation för c.
--------------
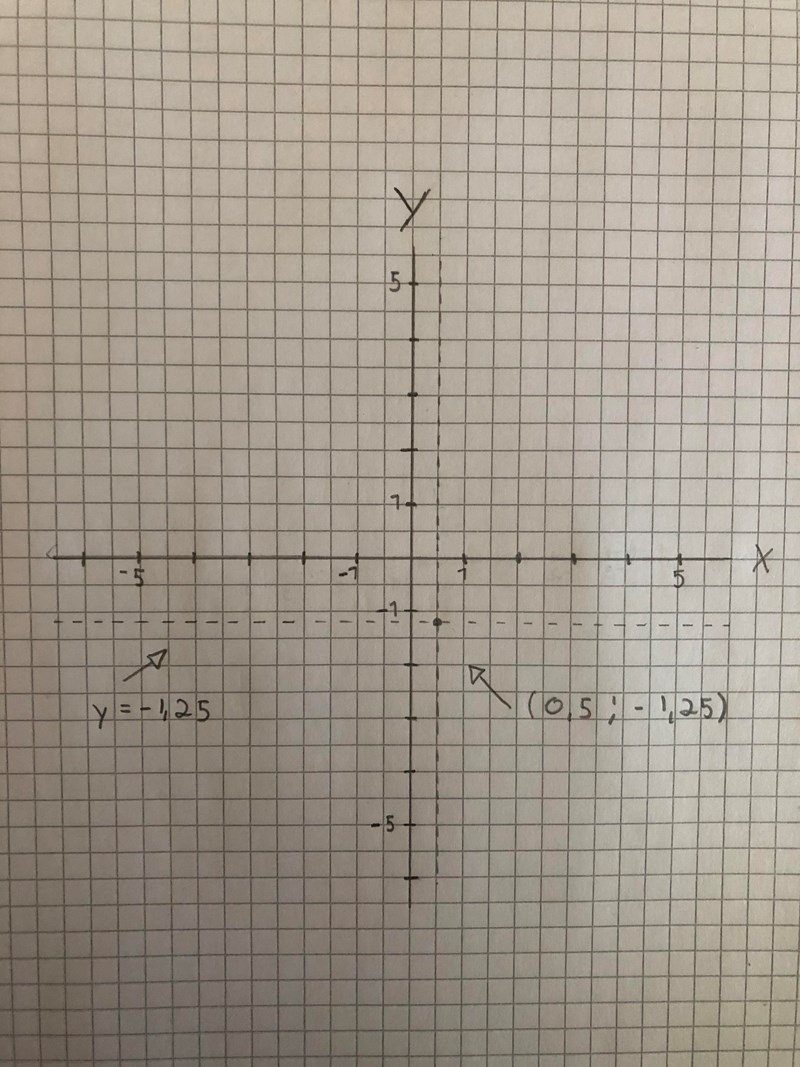
Här är en illustration av mitt tidigare tips.
Jag har ritat in symmetrilinjen x = 0,5 som en vertikall blå linje och en ungefärlig bild av parabeln. Jag har med rött markerat att f(-1) = f(2) och tydliggjort att dessa punkter ligger på var sin sida om och på samma avstånd från symmetrilinjen.
På grund av symmetrilinjens egenskaper så ger f(-1) = f(2) direkt att symmetrilinjen ligger mitt emellan x = -1 och x = 2.
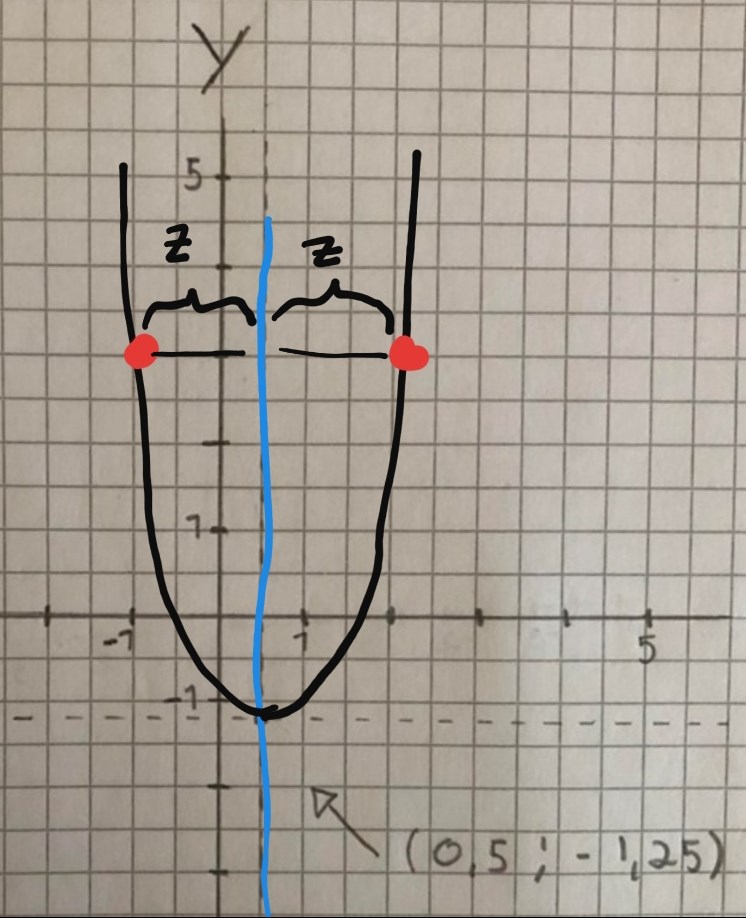
Tack tror jag löst det om jag tänkt rätt!
Det är ganska klottrigt men hoppas du är med.
Har fått att b=-x och c=-1.
f(x)= x2 -x -1
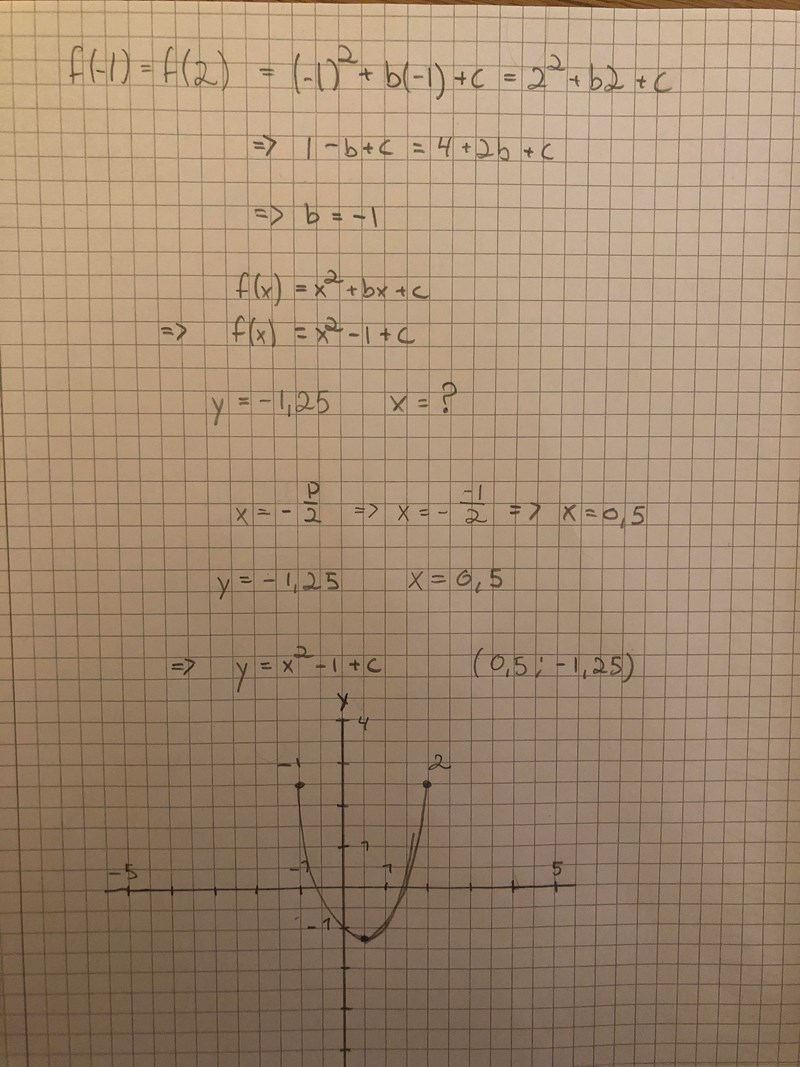
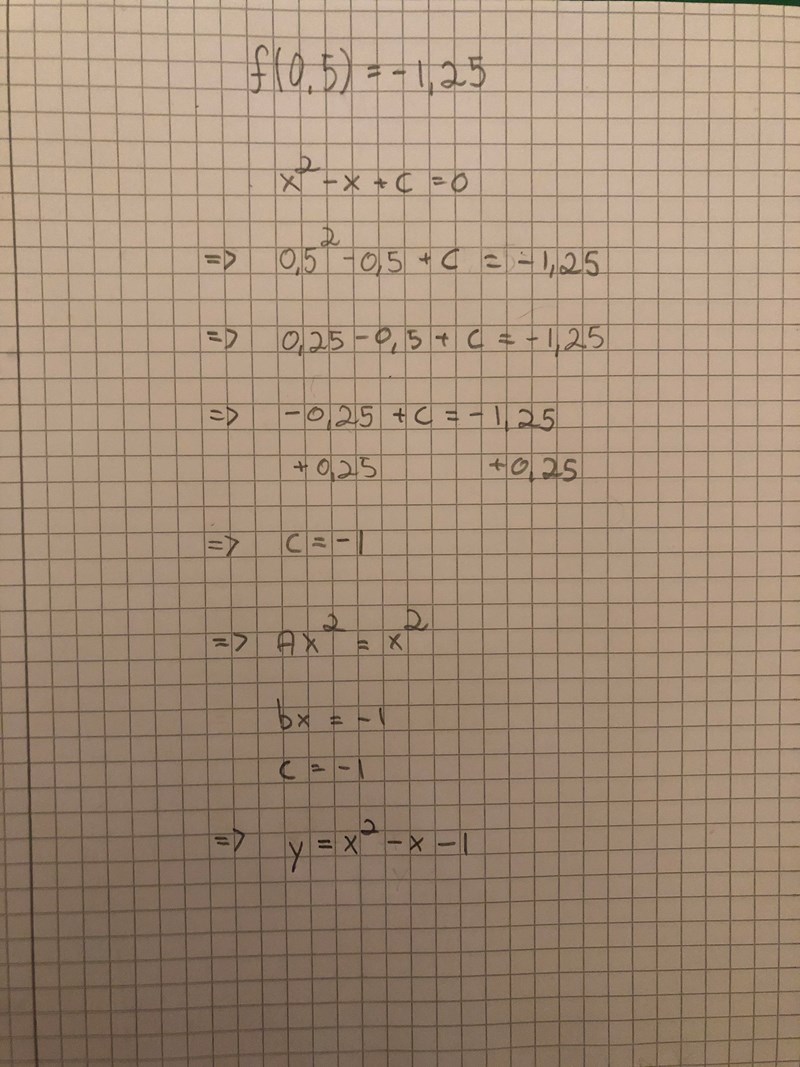
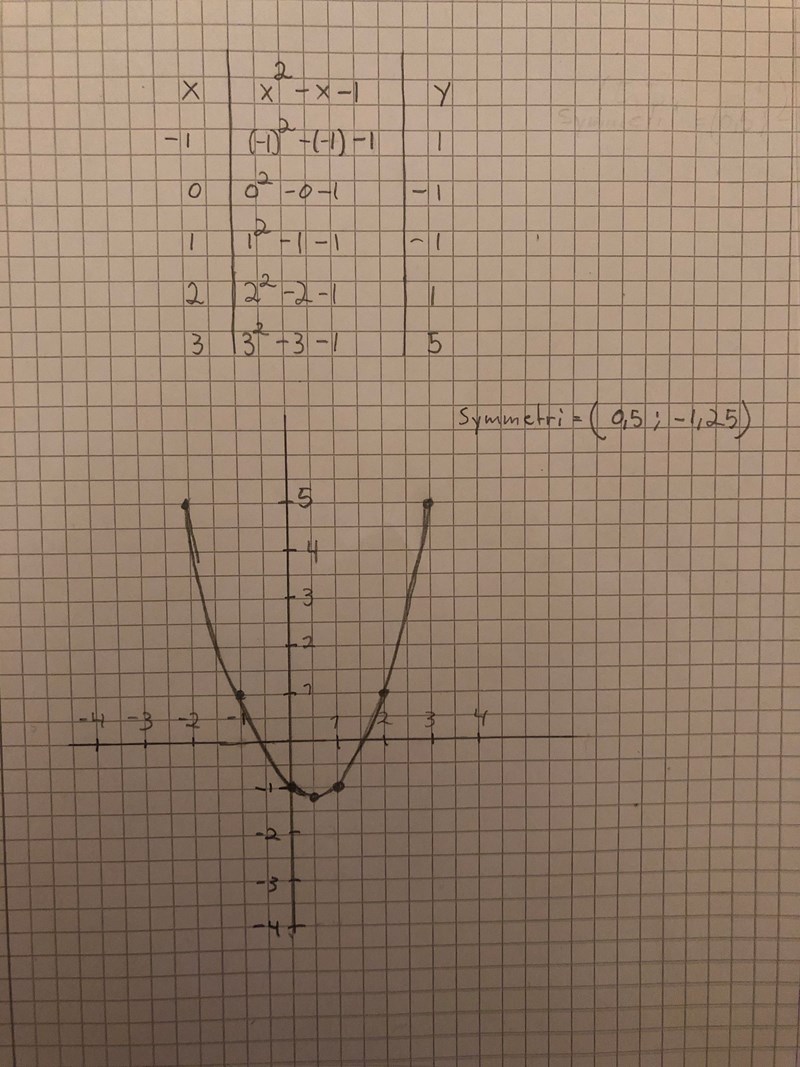
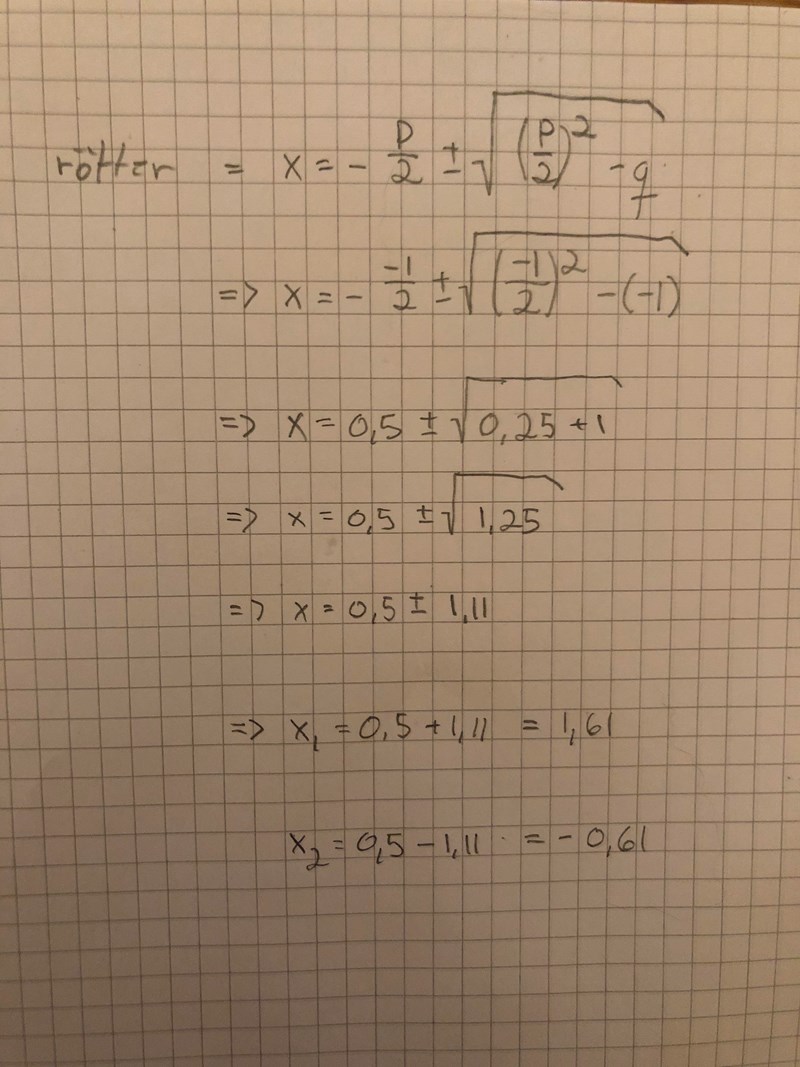
Ja det stämmer, men du har en del onödiga uträkningar.
Följande skulle räcka:

Ja det blev en hel del onödiga uträkningar, var kul att testa om allt stämde om jag ritade och jämförde grafen i Desmos.
Tack för hjälp, är ganska säker på att jag kommer kunna ta hjälp av detta i framtiden!






