Bestäm g’(3)
Hur löser jag detta? 🤔
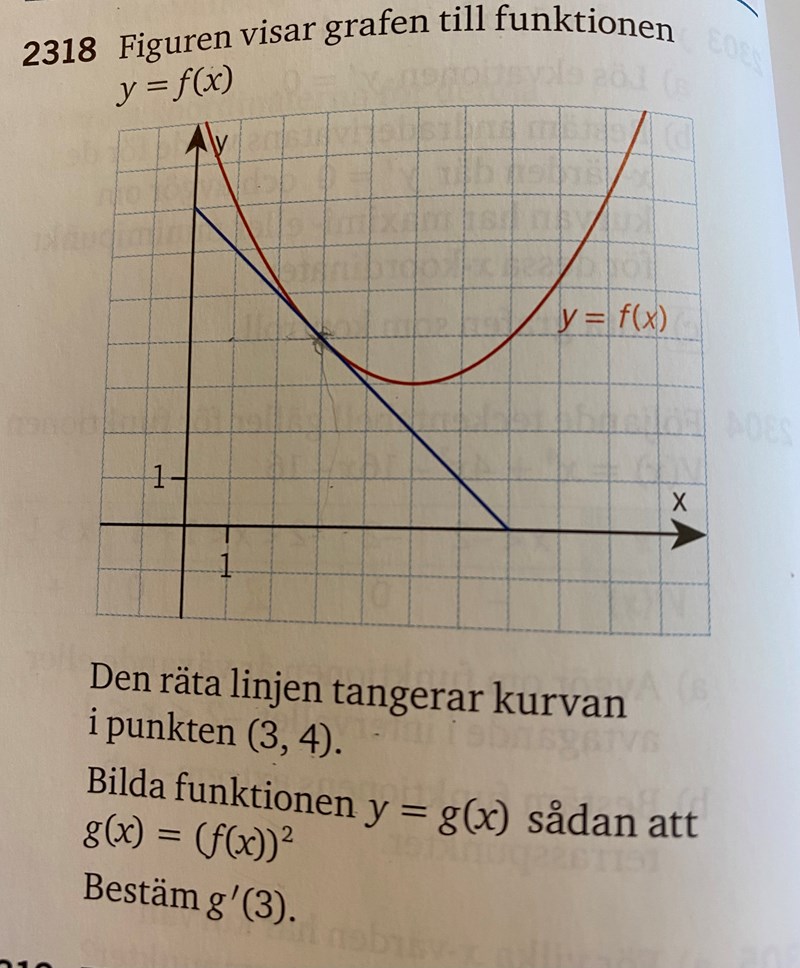 Bör jag försöka få fram funktionen för y=f(x)?
Bör jag försöka få fram funktionen för y=f(x)?
Sant, läs Smaragdalenas inlägg. Vi vet inte hur f(x) ser ut utanför bilden och kan därmed ej avgöra vilken typ av funktion det är (ser ju ut som en andragradare här men skulle kunna vara något annat)
Nej, det behövs inte, och vi kan inte veta säkert vad f(x) är. Det skulle kunna vara en andragradsfunktion, kanske. Vad är derivatan av den sammansatta funktionen g(x) = (f(x))2? Läs av lämpliga värden i grafen.
Okej. Men det är det jag inte förstår. Hur ska jag få fram vad derivatan är av g(x)? Eller menar du
g(x)=(f(x))^2 => g(x)=2(f(x))?
Hur deriverar du t. ex. ?
ilovechocolate skrev:Okej. Men det är det jag inte förstår. Hur ska jag få fram vad derivatan är av g(x)? Eller menar du
g(x)=(f(x))^2 => g(x)=2(f(x))?
Det stämmer inte, du har glömt inre derivatan.
Laguna skrev:Hur deriverar du t. ex. ?
Men det blir ju y= sin^2x = (sin x)^2 => y’=cos x • 2(sin x) = 2 cos x • sin x
Så ni menar att g(x)=(f(x))^2 => g’(x)= f’(x)•2f(x)=2f’(x)•f(x) ?
Just det.
Hur ska jag fortsätta? Blir det att man sätter in 3 i hela derivatan, dvs g’(3)=2f’(3)•f(3)?
ilovechocolate skrev:Hur ska jag fortsätta? Blir det att man sätter in 3 i hela derivatan, dvs g’(3)=2f’(3)•f(3)?
Ja.
Hur blir det sen då? Antar f(3)=4, och f’(3)=-1 (lutningen i den punkten är -1).
Gör man såhär då: g’(3)=2f’(3)•f(3)=2(-1)•4=-8?



