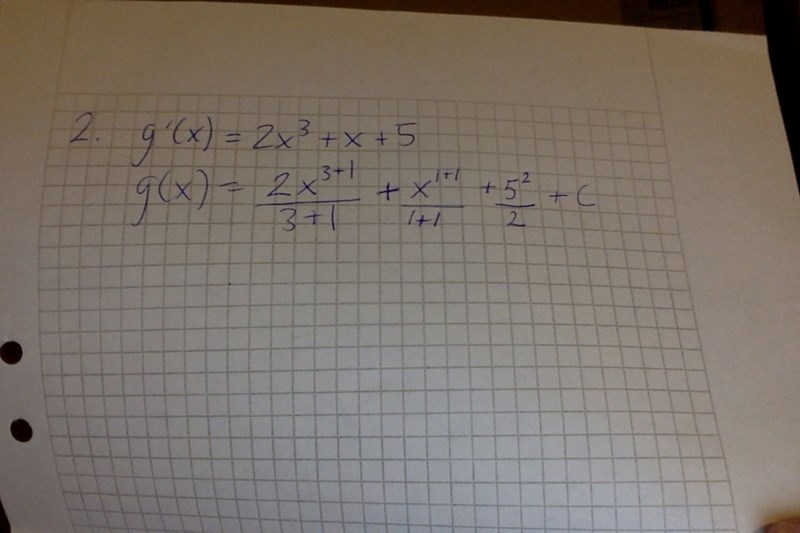Bestäm g(x) om du vet att funktionen går igenom origo
Hej! Jag behöver akuthjälp med en uppgift i matte 3. Såhär står det;
Bestäm g(x) om du vet att funktionen går igenom origo och att g´(x)=2x^3+x+5
Vill gärna ha förklaringar och motiveringar till svaren då jag ska redovisa denna uppgift imorgon och vet inte om jag räknat fel. Tack på förhand!
snälla hjälp!
Du vet g'(x). Hur kan du då få fram möjliga uttryck för g(x)? Du vet också att g(x) går genom origo.
Det jag tror att man ska räkna är omvänd derivata men sen då?
men jag har aldrig räknat med att en funktion går igenom origo därför blir jag osäker. Vad är lösningen egentligen ??
Vad får du om du gör så?
Vad är x- och y-värdena i origo?
x och y värdarna i origo är 0 men steget efter man räknat omvänd derivata (primitiva funktioner) vad händer sen?
Det kan vi ta när du har räknat ut din "omvända derivata".
hoppas du kan se bilden
Den är inte helt rätt! Tänk på att du alltid kan kontrollderivera. Vilken eller vilka termer är fel?
Kan du säga vad som är fel med den då?
Har du deriverat det uttryck för g(x) som du fick fram? Vad är derivatan av 12.5?
Välkommen.till Pluggakuten oliviaward!
Du bör.ta som vana.att alltid konttollera dina resultet.
När du tagit fram en primitiv funktion bör du derivera den och kontrollera att resultatet blir detsamma som ursprungsfunktionen.
Om F(x) är en primitiv funktion till f(x) så gäller att F'(x) = f(x).
Derivera alltså ditt uttryck för g(x) och kontrollera att du då får fram g'(x).
Tips: Skriv konstanten 5 som 5*x^0 innan du tar fram den primitiva funktionen.