Bestäm hjulets H_O och T
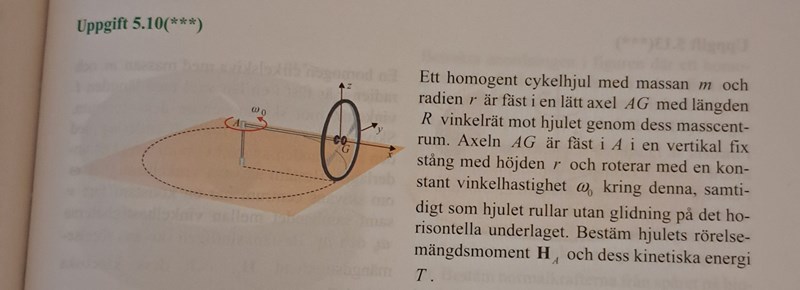
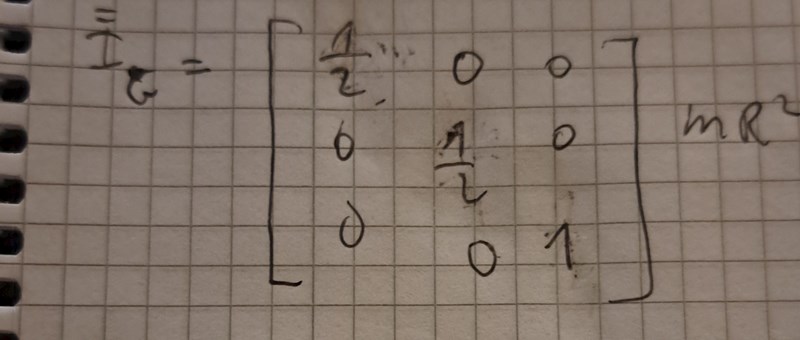
Jag började med att bestämma tensormatrisen och tänkte bestämma rörelsemängdsmomentet men fastnade i hur jag ska bestämma komponenter för vinkelhastigheten eftersom cykelhjulet har inte en vinkelhastighet som den roterar med. Sen ska vi ju ha tröghetsmoment map A och vet ej hur jag ska hitta det mha parallellförlfyttningssatsen. Hur tar man fram kroppens vinkelhastighet?
Antingen så tittar man på systemet som full rotation kring A. Men då behövs som du skriver tröghetsmatrisen map A. Lättare är kanske att kolla på rmm:s translation och rotationskomponent för sig. Oavsett är det viktigt att inse att hjulets masscentrum rör sig med hastigheten .
MrPotatohead skrev:Antingen så tittar man på systemet som full rotation kring A. Men då behövs som du skriver tröghetsmatrisen map A. Lättare är kanske att kolla på rmm:s translation och rotationskomponent för sig. Oavsett är det viktigt att inse att hjulets masscentrum rör sig med hastigheten .
Ja asså det är vad boken gör dvs tittar på full rotation kring en viss punkt och vi söker ju H_A så jag tänkte använda mig av parallellförflyttningssatsen för tröghetsprodukter men fastnade på hur jag ska göra där. Jag är lite inne på det tankesättet.
Hur vet man att hjulets masscentrum rör sig med w0?
Ja, man får bygga en matris för masscentrum och en matris för förflyttningen.
Tänkte fel med hastigheten. Den är såklart .
MrPotatohead skrev:Ja, man får bygga en matris för masscentrum och en matris för förflyttningen.
Tänkte fel med hastigheten. Den är såklart .
Hm hur bestämmer du den ? roterar inte w0 moturs dvs i ex riktning enligt figuren?
Matrisen för masscentrum har jag redan. Men det är den för punkten A som jag inte vet hur man ska få fram. Ska man bilda ett nytt koordinatsystem i A ? Denna formel gäller ju för att kunna ta fram den. Tröghetsprodukter i masscentrum är ju 0 så jag vet inte om man söker Ix'y'? mxGyG är väl mR^2?
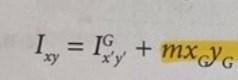
vG = w0ez x rAG = w0Rey.
whjul = w0ez + wxex.
No-slip-villkor: vG + whjul x (-rey) = 0. Ger wx = -w0R/r.
PATENTERAMERA skrev:vG = w0ez x rAG = w0Rey.
whjul = w0ez + wxex.
No-slip-villkor: vG + whjul x (-rey) = 0. Ger wx = -w0R/r.
1) Hur vet man att w0 roterar i ez ?
2)Varför skrivs whjul som en summa av wx och w0?
3)Hur vet man att wx är riktad i ex?
Din sista ekvation förstår jag inte. Är det v_A? Varför är den lika med 0?
1) Se figur. Högerhandsregeln.
2 och 3) Hjulets vinkelhastighet är vinkelhastigheten hos xyz-systemet (w0ez) + hjulets vinkelhastighet relativt xyz-systemet (wxex). wx är en obekant som vi beräknar med villkoret att hjulet rullar utan glidning. Det är det jag kallar no-slip-villkor. Alltså, hjulets kontaktpunkt med marken måste hela tiden ha hastigheten noll.
Man inser från geometrin att hjulets vinkelhastighet inte har en y-komponent. Men om du vill kan du göra en mera allmän ansats där du lägger till en term wyey till hjulets vinkelhastighet.
PATENTERAMERA skrev:1) Se figur. Högerhandsregeln.
2 och 3) Hjulets vinkelhastighet är vinkelhastigheten hos xyz-systemet (w0ez) + hjulets vinkelhastighet relativt xyz-systemet (wxex). wx är en obekant som vi beräknar med villkoret att hjulet rullar utan glidning. Det är det jag kallar no-slip-villkor. Alltså, hjulets kontaktpunkt med marken måste hela tiden ha hastigheten noll.
Man inser från geometrin att hjulets vinkelhastighet inte har en y-komponent. Men om du vill kan du göra en mera allmän ansats där du lägger till en term wyey till hjulets vinkelhastighet.
hm jag vet inte hur man ser med högerhandsregeln. Men man kan sätta koordinatsystem och då roterar den väl i ez?
Hm jag ser inte hur hjulets vinkelhastighet saknar y -komponent. Försökte hänga med i ditt uttryck med v_g men sen tappade jag bort dig där vid no slip villkor. Boken gjorde ungefär såhär också med en liknande exempel.
När man räknar fram v_g från A till G så är punkten A fix dvs v_A=0 medan i G så räknar från C till G då man vet att v_C=0 pga kontaktpunkt med marken.

Högerhandsregeln.
 Hjulet är vinkelrätt anordnat på axeln. Om det fanns en y-komponent så skulle hjulet vrida sig så att det inte längre var vinkelrät mot axeln. Vilket inte är tillåtet.
Hjulet är vinkelrätt anordnat på axeln. Om det fanns en y-komponent så skulle hjulet vrida sig så att det inte längre var vinkelrät mot axeln. Vilket inte är tillåtet.
Jag vet inte vad C är för det finns inte med i problemtexten.
PATENTERAMERA skrev:Högerhandsregeln.
Hjulet är vinkelrätt anordnat på axeln. Om det fanns en y-komponent så skulle hjulet vrida sig så att det inte längre var vinkelrät mot axeln. Vilket inte är tillåtet.
Jag vet inte vad C är för det finns inte med i problemtexten.
Ja ok. Så hjulet är vinkelrät mot axeln AG och då blir det bara wez och wx som komponenter som bildar hjulets w?
Nej jag vet. C är kontaktpunkten mellan hjulet och marken som man kan själv införa. Den är ju 0. De gjorde det i ett liknande problem i boken i sidan innan.
Jag vill använda parallellsatsen som de gjorde i en liknande uppgift nedan. Men hur kan jag få till det i mitt fall där jag har matrisen IG?

IA = IG + m() = IG + mR2(E-exex)=
IG + mR2.
PATENTERAMERA skrev:IA = IG + m() = IG + mR2(E-exex)=
IG + mR2.
Jag förstår inte hur du använder avståndet för parallellförflyttningsatsen och vad hela paretensen står för?
Man kan se Steiners sats som träghetsmomentet för en punktmassa. Element Ixx är avståndet till x-axeln, i detta fall är det 0, Iyy är avståndet till y-axeln (här det ) och Izz är avståndet till z-axeln (också ). Därför blir matrisen som den blir.
MrPotatohead skrev:Man kan se Steiners sats som träghetsmomentet för en punktmassa. Element Ixx är avståndet till x-axeln, i detta fall är det 0, Iyy är avståndet till y-axeln (här det ) och Izz är avståndet till z-axeln (också ). Därför blir matrisen som den blir.
Jag tror tyvärr inte att jag hänger med riktigt. Misstänker att han använde sig av enhetsmatrisen gånger |R|^2. Från A till G är det ju Rex . Jag undrar om han inte har glömt att skriva ( 1,0,0) i första kolonen av E. I facit så har Ixx en komponent som är nollskild för IA.
Ja, den totala matrisens xx-element är nollskilt eftersom det finns en tröghet att rotera själva hjulet kring x-axeln. Men när vi flyttar axeln så har vi samma avstånd till x-axeln innan och efter flytten. Alltså kommer det inte dyka upp något extra bidrag.
MrPotatohead skrev:Ja, den totala matrisens xx-element är nollskillt eftersom det finns en tröghet att rotera själva hjulet kring x-axeln. Men när vi flyttar axeln så har vi samma avstånd till x-axeln innan och efter vi flyttat tröghetspunkten. Alltså kommer det inte dyka upp något extra bidrag.
Jag får räkna exakt hur det blir för IA när jag kommer hem om inte pantermera hinner före. Sitter tyvärr på tåget nu. Återkommer.
PATENTERAMERA skrev:IA = IG + m() = IG + mR2(E-exex)=
IG + mR2.
Du råkar inte glömma en etta i första kolumnen av enhetsmatrisen vid mR^2 om jag tolkar din E-matris rätt? Mitt IA blir
[ 3/2 0 0
0 3/2 0
0 0 2 ] mR2
E-matrisen är ju
[ 1 0 0
0 1 0
0 0 1]
Facit håller ej med om IA matrisen så jag undrar hur man ska korrigera detta? Jag valde z-axeln so m symmetri för en cirkulär ring när jag tog fram IG men vet ej om sånt spelar roll för att hitta IA.
E är enhetsmatrisen/tensorn. Tensorprodukten mellan två vektorer definieras i indexform som (uv)ij = uivj.
Om du visar dina beräkningar så blir det lättare att se om något gått fel.
Mitt IA blir[ 3/2 0 0
0 3/2 0
0 0 2 ] mR2
Facit håller ej med om IA matrisen så jag undrar hur man ska korrigera detta? Jag valde z-axeln so m symmetri för en cirkulär ring när jag tog fram IG men vet ej om sånt spelar roll för att hitta IA.
Tänk på att så du kan inte slå ihop termer innehållande mr^2 med mR^2 (som det åtminstone ser ut som att du gjort).
D4NIEL skrev:Mitt IA blir[ 3/2 0 0
0 3/2 0
0 0 2 ] mR2
Facit håller ej med om IA matrisen så jag undrar hur man ska korrigera detta? Jag valde z-axeln so m symmetri för en cirkulär ring när jag tog fram IG men vet ej om sånt spelar roll för att hitta IA.
Tänk på att så du kan inte slå ihop termer innehållande mr^2 med mR^2 (som det åtminstone ser ut som att du gjort).
Hm ok. Jag förstår inte hur du har fått den matrisen. Sitter som ett stort frågetecken i flera timmar pga vad IA bör bli.
PATENTERAMERA skrev:Om du visar dina beräkningar så blir det lättare att se om något gått fel.
Jag kan ha missförstått hur detta ska vara. Men såhär tolkade jag det du skrev förut om IA. Jag skulle uppskatta om ni kan visa vad som är fel och hur det ska se ut osv. Det verkar en skillnad mellan R och lilla r här.
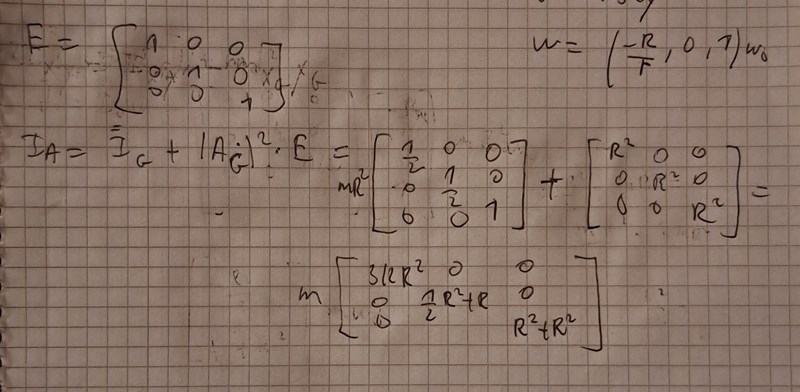
Hjulet snurrar runt x-axeln, du verkar ha lagt det runt z-axeln?
Sedan parallellförflyttar längden utmed x-axeln för att hitta , då blir matrisen
Slutligen är samt
D4NIEL skrev:Hjulet snurrar runt x-axeln, du verkar ha lagt det runt z-axeln?
Sedan parallellförflyttar längden utmed x-axeln för att hitta , då blir matrisen
Slutligen är samt
Men vänta varför blir det runt x-axeln? Hur vet man att den snurrar runt x-axeln? Varför stämmer inte mitt I_g där man har z-axeln som symmetriaxeln och vi har xy-planet? I boken är det ju såhär för Izz , Ixx och Iyy.


Frågan ger dig ett koordinatsystem så här:
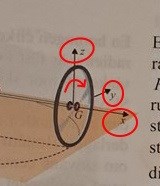
Hjulet ligger alltså "platt" i yz-planet. Här hoppas jag att man ser att hjulet snurrar (den röda pilens riktning) medurs sett från spetsen av -axeln. Det innebär att bidraget till från denna rotation blir , totalt sett blir .
När du ger ditt svar förväntas du använda det koordinatsystem som är givet i frågan. Man får såklart räkna i något annat system, bara man kommer ihåg att transformera sina svar i slutet av uppgiften. Men jag tror fortfarande att du blandar ihop med och jag tror det blir lättare för dig att räkna om du använder bilden och det givna koordinatsystemet redan från början.
D4NIEL skrev:Frågan ger dig ett koordinatsystem så här:
Hjulet ligger alltså "platt" i yz-planet. Här hoppas jag att man ser att hjulet snurrar (den röda pilens riktning) medurs sett från spetsen av -axeln. Det innebär att bidraget till från denna rotation blir , totalt sett blir .
När du ger ditt svar förväntas du använda det koordinatsystem som är givet i frågan. Man får såklart räkna i något annat system, bara man kommer ihåg att transformera sina svar i slutet av uppgiften. Men jag tror fortfarande att du blandar ihop med och jag tror det blir lättare för dig att räkna om du använder bilden och det givna koordinatsystemet redan från början.
ja det är just hur jag ska använda koordinatsystemet som ställer till. Hur kommer man på att hjulet snurrar till x-axeln? Jag kan typ ej se detta framför mig. Jag förstår att uppgiften gav oss ett koordinatsystem som vi använder men det är just hur man ska tänka med tröghetsmoment som jag fastnar över eftersom i bokens bild har de ett xy-plan och då räknar de ut Iz som mR^2. Tröghetskomponenterna verkar typ byta plats beroende på vilket koordinatsystem man tittar på. Här kanske jag inte riktigt ser att snurrande är kring x-axeln som du visar med pilen. Jag tänkte att hjulet måste snurrar kring z-axeln såsom den ser ut , men i din röda pil medurs så snurrar den även från z axeln till x-axeln." Hjulet ligger alltså "platt" i yz-planet. Här hoppas jag att man ser att hjulet snurrar (den röda pilens riktning) medurs sett från spetsen av x-axeln" här ser jag inte att hjulet ligger platt i yz-planet samt att den snurrar från spetsen. Kan du förtydliga hur du ser detta?
Hur bestämmer man kring vilken axel den snurrar runt? Är det via högerhandsregeln?
Som vi sagt tidigare. Hjulets vinkelhastighet är xyz-systemets vinkelhastighet plus hjulets vinkelhastighet relativt xyz-systemet.
, där är vinkelhastigheten relativt xyz-systemet. Du använder no-slip-villkoret, samt att hjulet är vinkelrät mot axeln, för att bestämma .
PATENTERAMERA skrev:Som vi sagt tidigare. Hjulets vinkelhastighet är xyz-systemets vinkelhastighet plus hjulets vinkelhastighet relativt xyz-systemet.
, där är vinkelhastigheten relativt xyz-systemet. Du använder no-slip-villkoret, samt att hjulet är vinkelrät mot axeln, för att bestämma .
Fast jag förstår inte vad detta har att göra med att bestämma tröghetstensormatrisen Ig ? vi har en zyx system i vår figur. Jag bestämde bara I_g utifrån #26 bilderna, men detta verkar inte stämma med uppgiftens koordinatsystems tensormatris gällande komponenterna.
Nej, just det. I det fallet har du en plan figur i xy-planet. Nu har du en plan figur i yz-planet. Men du kan enkelt använda satsen mutatis mutandis genom att inse att i detta fall så spelar x-axeln samma roll som z-axeln i boken.
PATENTERAMERA skrev:Nej, just det. I det fallet har du en plan figur i xy-planet. Nu har du en plan figur i yz-planet. Men du kan enkelt använda satsen mutatis mutandis genom att inse att i detta fall så spelar x-axeln samma roll som z-axeln i boken.
Ja precis. Men hur vet vi att vi har en yz-plan? När man tittar på det här hjulet så är y-axeln riktad bort från oss och det ser mer ut som att vi har zx-plan och då spelar y-axeln samma roll som z-axeln i boken.
Nej, hjulet ligger ju plant i yz-planet här och x-axeln är vinkelrät mot detta plan. I boken så är föremålet plant i xy-planet och z-axeln är vinkelrät.
PATENTERAMERA skrev:Nej, hjulet ligger ju plant i yz-planet här och x-axeln är vinkelrät mot detta plan. I boken så är föremålet plant i xy-planet och z-axeln är vinkelrät.
Ja precis z-axeln är vinkelrät mot xy-planet. Så bara för att x-axeln är vinkelrät mot z-axeln så måste den vara vinkelrät i sin tur mot zy-planet och då ligger hjulet i zy-planet om jag förstått detta rätt när du säger hjulet ligger plant i yz-planet?
Att hjulet ligger i yz-planet syns ju i figuren.
PATENTERAMERA skrev:Att hjulet ligger i yz-planet syns ju i figuren.
Nja för mig syns det inte det med zyx koordinatsystem om du syftar på den svarta hjulet. Jag tittade faktiskt på bilden flera gånger.
Hjulet är ju vinkelrät mot axeln AG (enligt texten) som är parallell med x-axeln. Eftesom, x-axeln är vinkelrät mot yz-planet så ligger hjulet således i yz-planet.
PATENTERAMERA skrev:Hjulet är ju vinkelrät mot axeln AG (enligt texten) som är parallell med x-axeln. Eftesom, x-axeln är vinkelrät mot yz-planet så ligger hjulet således i yz-planet.
Ja det var ju det jag skrev i #34. Om x axeln är vinkelrät mot y-axeln samt z-axeln så måste det innebära att x -axeln är vinkelrät i sin tur mot yz-planet.
Korrekt.
PATENTERAMERA skrev:Korrekt.
Varför får Ixx inget bidrag och de andra tröghetsmomenten får det när den parallellförflyttas till AG? Är det för att vi är yz-planet?
Precis. där både och är 0.
MrPotatohead skrev:Precis. där både och är 0.
Hur är de 0? Vad blir integranden? Det är just det jag inte förstår. När man bestämmer Ixx map på g så är det ju som vi snackat sen innan mr^2 för Ixx , 1/2mr^2 för Iyy och 1/2mr^2 för Izz. För z-axeln kan jag förstå att den får ett bidrag vinkelrät mellan z-axeln i G och i A , men för y och x ser jag inte varför det inte blir bidrag för något av dem.
Chat säger att det borde bli m(r^2+R^2) för Ixx komponenten av IA men jag är tveksam pga de senare konversationerna vi har haft så vill bli extra övertygad.
Jag tänker det makear sense att Izz för A har dz=R+r (vinkelrät avstånd) men jag ser inte hur det blir för y och x när man ska finna det vinkelräta avståndet från G till A. Jag försökte med denna figur men det blev ganska jobbigt att tänka sig.
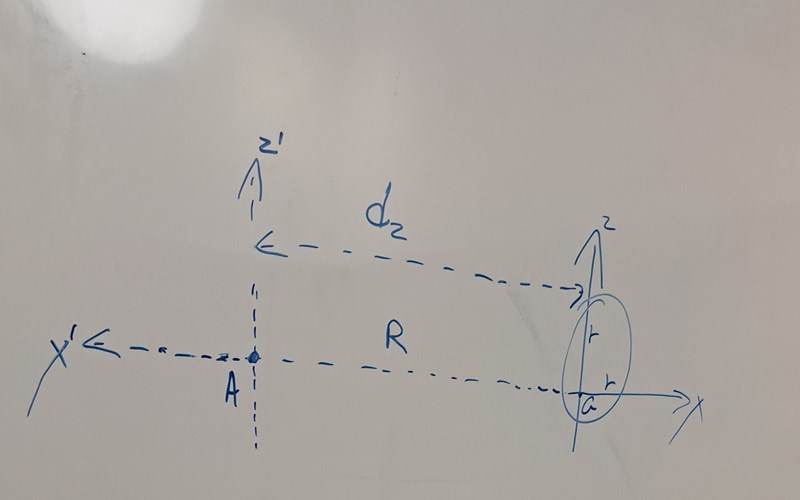
Jag kanske är otydlig. har tröghetsmomentet man hittar i en formeltabell, eller härleder, där alla diagonala element är nollskilda. Är du med så långt?
Steiners sats kan du se som att du lägger behandlar G som punktmassa map A. Eftersom det inte är någon skillnad på massans fördelning kring x-axeln i G eller A kommer inte Steiners sats ge något bidrag där.
MrPotatohead skrev:Jag kanske är otydlig. har tröghetsmomentet man hittar i en formeltabell, eller härleder, där alla diagonala element är nollskilda. Är du med så långt?
Steiners sats kan du se som att du lägger behandlar G som punktmassa map A. Eftersom det inte är någon skillnad på massans fördelning kring x-axeln i G eller A kommer inte Steiners sats ge något bidrag där.
Ja asså jag är med på vad IG har för komponenter på diagonalen. Det är inte det jag stör mig på. Det är mer hur man ska tänka för att få de här bidrag för IA mha parallellförflyttningssatsen såsom Daniel har fått fram i #22. Jag kan se att i z-led från z till z' axeln så blir Izz,A= m(R2+r2)/2 ,men jag vet ej hur man ska resonera för yy och xx komponent visuellt.
D4NIEL skrev:Hjulet snurrar runt x-axeln, du verkar ha lagt det runt z-axeln?
Sedan parallellförflyttar längden utmed x-axeln för att hitta , då blir matrisen
Slutligen är samt
Vill du visa hur du resonerar när du parallellförflyttar Ixx och Iyy från G till A om du använder parallellförflyttningssatsen? Jag tänker i z-led ser man tydligt att vinkelräta avståndet d är R+r från G till A. Jag försökte resonera på samma sätt med y och x komponenterna men jag får inget vinkelrät avstånd där.
Du menar väl att avståndet är R?
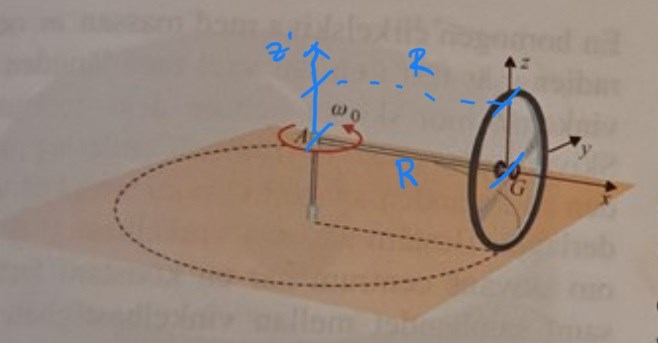
Ah, det kanske missförståndet är. För kollar vi på massfördelningen runt x-axeln och INTE avståndet i x-led. Du kan tänka på flyttningssatsen som det avstånd vi flyttar koordinataxlarna från G till A. x-axeln flyttas ingenting och således kommer flyttningen inte ge något bidrag till . Dock flyttas både y- och x-axeln , vilket motsvarar ett extra bidrag till både och .
PATENTERAMERA skrev:Du menar väl att avståndet är R?
Ja exakt avståndet är R från Z till Z' och då tänker jag att Izz får det här bidraget m(R^2+r^2)
(IA)zz = (IG)zz + mR2 = (1/2)mr2 + mR2
PATENTERAMERA skrev:(IA)zz = (IG)zz + mR2 = (1/2)mr2 + mR2
Ja precis jag glömde att det ska vara delat på 1/2 sorry. Enligt din bild i #47 så verkar det vinkelräta avståndet från y till y' vara R och för x så är x' på samma axel som x så där saknas det vinkelräta avståndet d.



