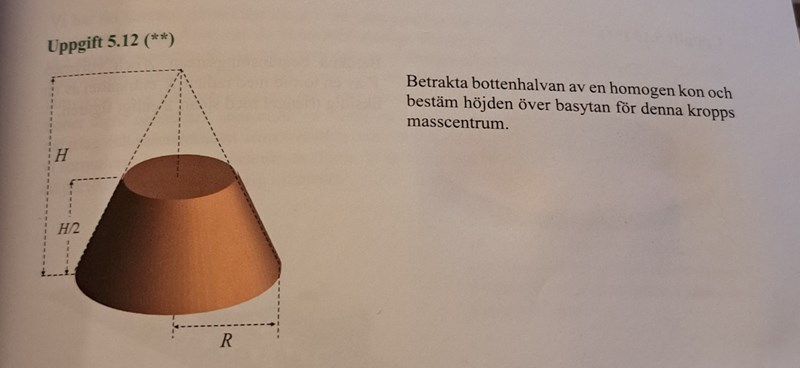
Bestäm höjden över basytan för denna kropps masscentrum

Du behöver bara kunna masscentrum för en kon i den här uppgiften. Konens masscentrum ligger 1/4 från basen. Kanske kan den här bilden ge dig en ledtråd om hur man kan tänka 

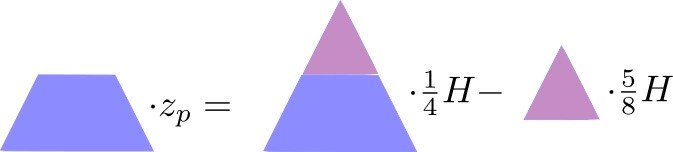
Det går också att lösa med en volymintegral i cylinderkoordinater. Men då måste du först skapa en funktion för hur den maximala radien $r$ varierar med höjden z i konen så du får rätt gränser för $r$ i integralen. Sedan gäller standardformeln för tyngdpunkter:

$V_{tot} \cdot z_p  = \iiint z rdrd\phi dz$

med korrekta gränser.

D4NIEL skrev:

Du behöver bara kunna masscentrum för en kon i den här uppgiften. Konens masscentrum ligger 1/4 från basen. Kanske kan den här bilden ge dig en ledtråd om hur man kan tänka 

Det går också att lösa med en volymintegral i cylinderkoordinater. Men då måste du först skapa en funktion för hur den maximala radien $r$ varierar med höjden z i konen så du får rätt gränser för $r$ i integralen. Sedan gäller standardformeln för tyngdpunkter:

$V_{tot} \cdot z_p  = \iiint z rdrd\phi dz$

med korrekta gränser.

Men i boken så är masscentrum för kon 3/4H? Jag är ej med på din figur tyvärr. Jag tänkte lösa med standardsättet dvs använda mig av sats för  sammansatt kropp men då vet jag inte hur man hittar masscentrum för bortskurna halvkon på korrekt sätt. Jag trodde dennes masscentrum var 3H/8,men facit håller inte med.

1/4H Från basen eller 3/4H från toppen av konen. Det är ju samma sak

D4NIEL skrev:

1/4H Från basen eller 3/4H från toppen av konen. Det är ju samma sak

Nu är jag inte med på hur de är samma sak?

Om man mäter avståndet mellan basytan och tyngdpunkten i en rak cirkulär kon är avståndet $\frac14 h$.

Om man istället mäter avståndet mellan toppen av konen och tyngdpunkten är avståndet $\frac34 h$.

Är du med?

Den bortskurna konen (toppkonen) har basradien R/2 och och dess tyngdpunkt ligger på H/2 + dess egen tyngdpunkt i den totala figuren.

D4NIEL skrev:

Om man mäter avståndet mellan basytan och tyngdpunkten i en rak cirkulär kon är avståndet $\frac14 h$.

Om man istället mäter avståndet mellan toppen av konen och tyngdpunkten är avståndet $\frac34 h$.

Är du med?

Den bortskurna konen (toppkonen) har basradien R/2 och och dess tyngdpunkt ligger på H/2 + dess egen tyngdpunkt i den totala figuren.

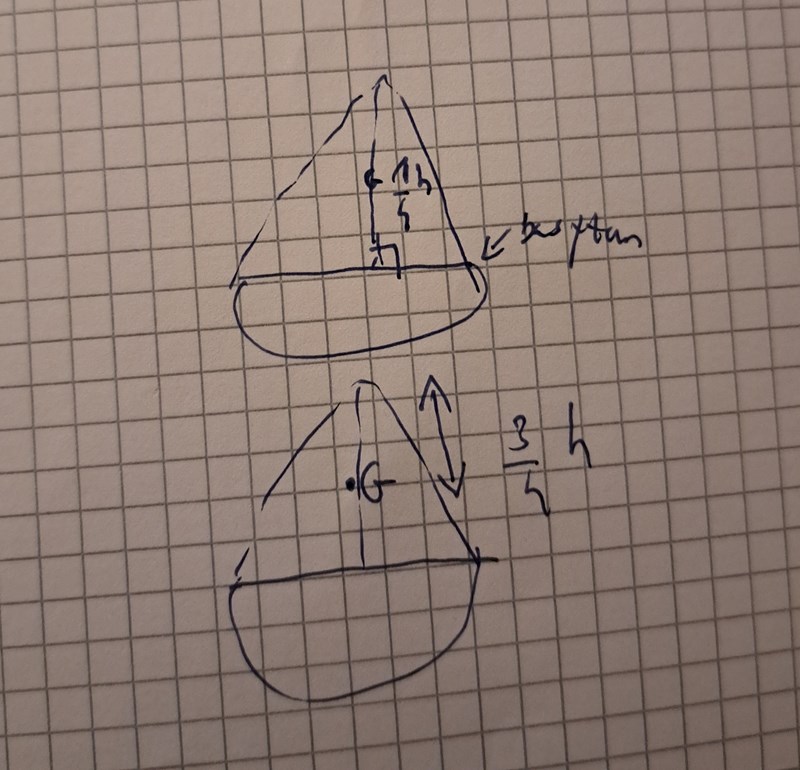
Jag antar att du menar såhär för konen om man mäter från basytan till tyngdpunkten eller från tyngdpunkten till toppen av konen när det gäller masscentrum för konen?

Ja, just det! Och jag tror det är enklast för dig att alltid mäta från basytan i uppgiften. Eftersom det är det de frågar om (den stympade konens tyngdpunkt över basytan)

"Den bortskurna konen (toppkonen) har basradien R/2 och och dess tyngdpunkt ligger på H/2 + dess egen tyngdpunkt i den totala figuren"

Hur kan man i figuren avläsa att R/2 är basradien för bortskurna konen och tyngdpunkten ligger H/2+dess egen tyngdpunkt?

Eftersom den maximala radien går linjärt från $r=R$ vid botten till $r=0$ i toppen $h=H$ av den stora konen kommer radien av symmetri vara $r=R/2$ då vi är vid höjden $H/2$. 

Men om du inte "ser" det måste du räkna ut en formel för hur radien $r$ varierar med höjden $h$ i konen. Det är en linjär funktion med

$r(0)=R$

$r(H)=0$

Och då visar det sig att $r(H/2)=R/2$

D4NIEL skrev:

Eftersom den maximala radien går linjärt från $r=R$ vid botten till $r=0$ i toppen $h=H$ av den stora konen kommer radien av symmetri vara $r=R/2$ då vi är vid höjden $H/2$. 

Men om du inte "ser" det måste du räkna ut en formel för hur radien $r$ varierar med höjden $h$ i konen. Det är en linjär funktion med

$r(0)=R$

$r(H)=0$

Och då visar det sig att $r(H/2)=R/2$

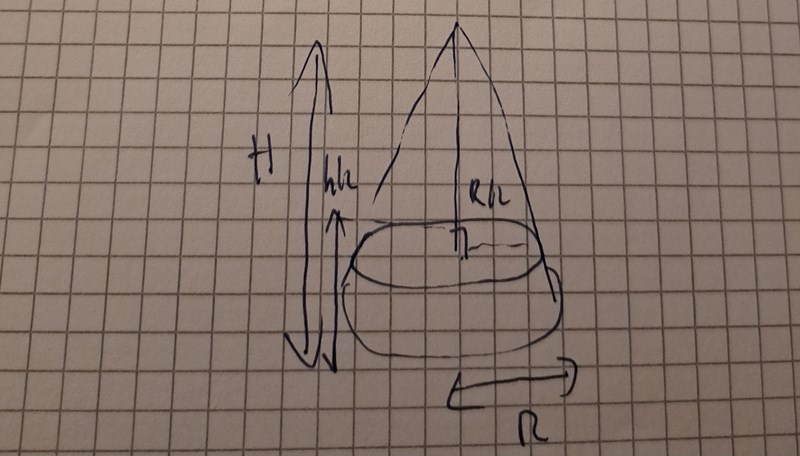
Men det enda jag kan tänka mig är att basradien för lilla konen är R/2. Eftersom den lilla konen har masscentrum H/8 dvs hälften av den stora så blir den totala masscentrum för den lilla h/2+h/8?

Ja, så den lilla konen har en basradie R/2, och dess höjd är H/2. Tyngdpunkten över den lilla konens basyta är $\frac14 \cdot H/2$

Eftersom den lilla konens basyta själv befinner sig på höjden $H/2$ blir alltså den lilla konens tyngdpunkt 

$H/2+\frac14 H/2$

Är du med?

D4NIEL skrev:

Ja, så den lilla konen har en basradie R/2, och dess höjd är H/2. Tyngdpunkten över den lilla konens basyta är $\frac14 \cdot H/2$

Eftersom den lilla konens basyta själv befinner sig på höjden $H/2$ blir alltså den lilla konens tyngdpunkt 

$H/2+\frac14 H/2$

Är du med?

Jag är inte med på varför man slår ihop tyngdpunkten för den lilla konen med höjden som den är på  ? Lösningsförslaget gör på det sättet men det förstår jag inte. Vad är konens basyta här?

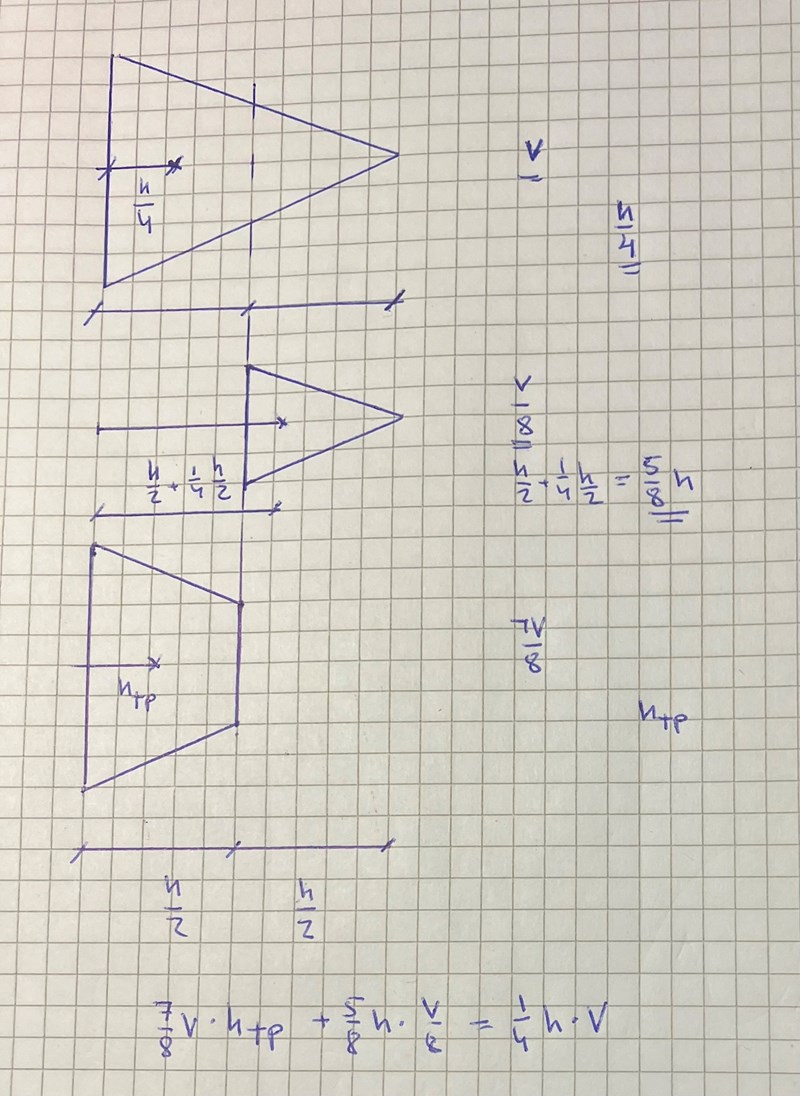
Se figur:

Sätt hela volymen till V och hela höjden till h

Tyngdpunkten för hela konen är h/4

Tyngdpunkten för lilla konen är h/2+1/4*h/2  och den lilla volymen är V/8 (alla de tre måtten radie gånger radie gånger höjd är hälften vardera, "volymskalan är kuben på längdskalan")

Restvolymen är då 7/8V och den sökta höjden h _TP

Regeln för beräkning av tyngdpunkt ger då ekvationen nederst i figuren (samma som i #2)

ur vilken h_TP kan lösas ut.