Bestäm intervall för ytintegralen Y

Hej! Jag har en uppgift där jag skall beräkna ytintegralen :

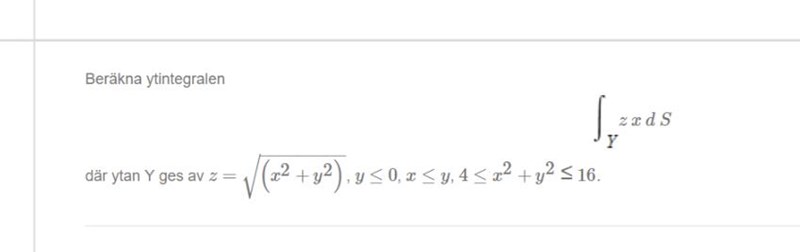
mitt r blir då r(t) = (x,y,sqrt(x^2+y^2))

där jag kan annvända denna formel

$\iint F d s = \int_{a}^{b} \int_{c}^{d} F (r (s, t)) * ∥ \partial r / \partial s \times \partial r / \partial t ∥$

där det blir

$\int_{a}^{b} \int_{c}^{d}$ sqrt(2)

men jag får inte riktigt till intervallen a,b,c och d. funderar om den ena gränsen är mellan 0 och x eftersom x<=Y<=0. Skulle nån kunna hjälpa mig

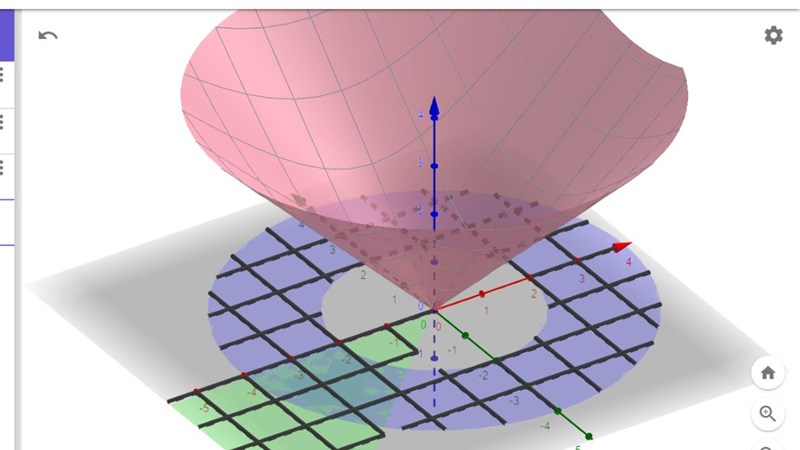
Standardfråga 1a: Har du ritat?

Ritat upp ytan som du skall integrera över, alltså.

jo jag har ritat upp frågan och bytte till cylindriska koordinater men får fel. mitt svar är -60/sqrt(2) medans svaret -60. och jag förstår inte varför. kan någon förklara det :)

I ditt första inlägg har du ju räknat ut att det skall bli en faktor $\sqrt{2}$ i kryssprodukten av derivatorna, men vart tar denna vägen i din lösning?

(Jag skulle inte kalla $r$ :et för jacobian, jag skulle snarare säga att kryssprodukten av derivatorna är lika med $\sqrt{2}r$ , och att vi därför får ett extra $r$ )

Svara

Visa senaste svar