Bestäm konstanten
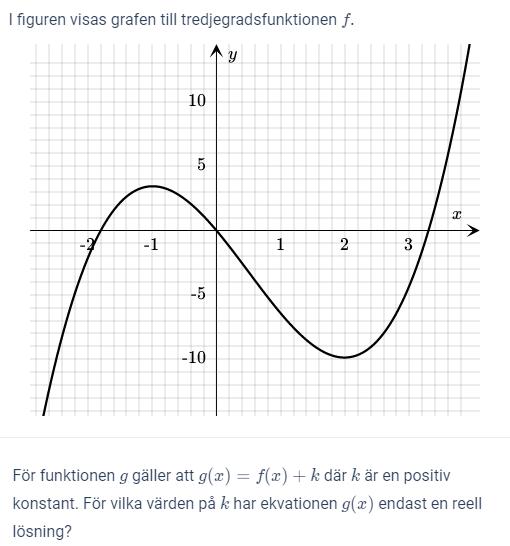
Jag vet att f(x)=(x-1)(x-2,8)(x+2,3) därmed borde
f(x)=k((x-1)(x-2,8)(x+2,3)) = en reel lösning
multiplicerar jag in parentesen får jag
k(x3-1,5x2-5,94x+6,44)
Hur fick du din formel? Den stämmer inte med att kurvan går genom origo.
Precis som Laguna skriver så stämmer inte det du har skrivit. För att hitta konstanten k ska du välja ytterligare en punkt som inte är ett nollställe
Laguna skrev:Hur fick du din formel? Den stämmer inte med att kurvan går genom origo.
den hade en a uppgift innan denna b uppgift och svaret på a var att f(x) har nollställerna x=1 x=2,8 och x=-2,3, det stämmer överens med facit
Är du säker på att det är samma uppgift,
Om du ser på grafen har funktionen nollstället x=0
ja, det är samma uppgift, a uppgiften var att lösa f(x)+6.5=0 och det är samma graf
Då är det inte f(x) som har de nollställena, utan f(x)+6,5.
För att hitta svaret på frågan kan du ta en linjal och lägga den parallellt med x-axeln på ett sådant sätt att den skär kurvan precis en gång.
10>y>3,5
y > 3,5 håller jag med om (men det är egentligen k), men inte 10 > y. Hur fick du det?
menar -10
för när den är -11 tex så skär den kurvan vid ett ställe bara, x=-2,6
Så vilka värden på k är svaret på frågan?
-3,5>k>10
Tänk på vad det står. k ska alltså vara mindre än -3,5 och större än 10. Det går inte.
Den flyttas ju 3,5 steg eller mer neråt och 10 steg eller mer uppåt, så det 3,5 så de 3,5 måste skrivas som minus 3,5. Det måste vara mindre än det då -2,5 ex ger 2 lösningar. Det måste också vara mer 10 på andra sidan hur ska jag då skriva
Du har kommit fram till rätt svar, men det som återstår är att formulera det matematiskt. Kan du göra det med två separata olikheter?
k<-3,5 eller >10
Ja, nu är jag nöjd, men det kan hända att läraren vill att du ska ha med k i den andra olikheten också.
Hur det mest accepterade sättet att sammanfatta två intervall med olikheter ser ut har jag faktiskt glömt.



