Bestäm konstanten A så att limx->inf = 1/7
Hej! Kommer in med en till uppgift ifrån nationella provet 2013 i Ma 3c. Såhär ser den ut:
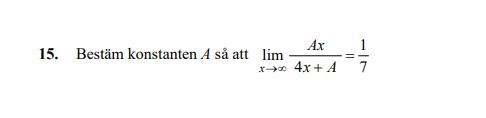
Jag löste denna såhär:
Det ska stå 4x/7x på näst sista raden... vet inte hur man redigerar.
Dock så hade smartare hjärnor än mig ett mycket smidigare sätt att lösa den på. De gjorde nämligen såhär:
Så till detta har jag två frågor:
1. Kan min lösning anses vara rätt? För mig känns det rätt att -1 blir försumbart när x blir större i 4x/(7x-1). Samtidigt syns det kanske bättre när x är direkt under A som nämnare? ( och dels känns mitt sätt väldigt dumt nu i efterhand )
2. Stoppar man in A=4/7 i ekvationen så håller inte likheten.
Jag antar ju att detta härstammar från att det är något jag inte förstår om gränsvärden... dock vet jag inte vad. Hade någon kunnat upplysa mig om vad det är jag missar vore jag evigt tacksam! (:
Problemet är att ett gränsvärdesuttryck inte är detsamma som en ekvation och därför inte kan lösas med 'vanliga' ekvationsregler.
Du kan se det i din lösning där du mot slutet har bråket 4x/7x och menar att du kan förkorta bort x.
Men och vad blir oändligheten dividerad med oändligheten?
Utan du får arbeta med lim-uttrycket utan att blanda in högerledet (1/7) så att du får x i några nämnare, vars gränsvärde går mot 0 då x går mot oändligheten. Så din lösning är inte korrekt vilket 'den smarta' lösningen är
Jag skulle helt enkelt ha tänkt i ursprungsekvationen:
Men resonemanget måste bygga på att man bara behåller de termer som växer snabbast.
För att återkoppla lite till Hennings kommentar. Jag ser egentligen inget problem att konstatera att -1 kan försummas jämfört med de termerna som innehåller x.
Den alternativa lösningen gör samma antagande, men ett steg innan.
Gränsvärdesproblemet är inte en likhet förrän x går mot gränsvärdet, därför kan man inte kontrollera sitt svar på det sättet som du försöker göra. Svaret på gränsvärdesproblem kontrolleras enklast genom att sätta in några x-värden som närmar sig gränsvärdet, och se vad man får. Då får man också lättare en känsla för vartåt kurvan drar, och vilka termer som blir dominanta.
I detta fallet, antag x=10
antag x=1000
antag x=1000000
Henning skrev:Problemet är att ett gränsvärdesuttryck inte är detsamma som en ekvation och därför inte kan lösas med 'vanliga' ekvationsregler.
Du kan se det i din lösning där du mot slutet har bråket 4x/7x och menar att du kan förkorta bort x.
Men och vad blir oändligheten dividerad med oändligheten?Utan du får arbeta med lim-uttrycket utan att blanda in högerledet (1/7) så att du får x i några nämnare, vars gränsvärde går mot 0 då x går mot oändligheten. Så din lösning är inte korrekt vilket 'den smarta' lösningen är
Hade ingen aning om att oändligheten / oändligheten är odefinierad.
Dock är jag förvirrad. Hoppas inte jag är för jobbig med mina frågor men har fått lite motstridig info, när jag googlade så säger vissa att infinity / infinity är odefinierat men att inom kontexten av gränsvärden så ska man faktorisera ut variablerna som går mot oändligheten och dividera koefficienterna som i uppgiften ( källan på detta är reddits ACT subreddit så ta det med den mängd salt du anser lämplig! )
Dock, så med det i åtanke och som JohanF nämnde ovan så verkar det som att vi gör samma antagande i den " smarta " lösningen, där vi dividerar bort x ifrån 4x termen i nämnaren. Hur kommer det sig att det går då? :s
Henning skrev:Du kan se det i din lösning där du mot slutet har bråket 4x/7x och menar att du kan förkorta bort x.
Men och vad blir oändligheten dividerad med oändligheten?
Att evaluera innebär inte att du får oändligheten dividerad med oändligheten. Kvoten närmar sig 1 snabbare än vad nämnare eller täljare växer. Gränsvärdet är identiskt lika med 1.
Som JohanF skrev så är detta ett faktum som den "smarta" lösningen använder sig av.
Utan du får arbeta med lim-uttrycket utan att blanda in högerledet (1/7) så att du får x i några nämnare, vars gränsvärde går mot 0 då x går mot oändligheten. Så din lösning är inte korrekt vilket 'den smarta' lösningen är
Detta behövs inte. Du har att och denna approximation går mot en likhet i gränsvärdet.
JohanF skrev:Gränsvärdesproblemet är inte en likhet förrän x går mot gränsvärdet, därför kan man inte kontrollera sitt svar på det sättet som du försöker göra.
Aha, det låter rätt logiskt nu när du säger det.
Den alternativa lösningen gör samma x/x=1antagande, men ett steg innan.
Nu är jag ännu mer förvirrad! Så har läst nu att infinity/infinty är odefinierat, men vissa ( på reddit ) säger att när man pratar om gränsvärden så kan man räkna bort x värdena som i i uppgiften. Och som du säger gör man ju det i den andra lösningen också. Jag har inte riktigt kunskapen för att säga vad som är rätt eller fel. Dock så tänker jag att när man räknar limx->oändligheten så räknar man väl inte med själva oändligheten, utan med ett konstant växande x och ser vilket värde uttrycket tenderar mot? Jag har kanske helt fel i hur jag tänker, och jag hör gärna varför jag har fel! Uppskattar all hjälp :)
Ebola skrev:Henning skrev:Du kan se det i din lösning där du mot slutet har bråket 4x/7x och menar att du kan förkorta bort x.
Men och vad blir oändligheten dividerad med oändligheten?Att evaluera innebär inte att du får oändligheten dividerad med oändligheten. Kvoten närmar sig 1 snabbare än vad nämnare eller täljare växer. Gränsvärdet är identiskt lika med 1.
Som JohanF skrev så är detta ett faktum som den "smarta" lösningen använder sig av.
Utan du får arbeta med lim-uttrycket utan att blanda in högerledet (1/7) så att du får x i några nämnare, vars gränsvärde går mot 0 då x går mot oändligheten. Så din lösning är inte korrekt vilket 'den smarta' lösningen är
Detta behövs inte. Du har att och denna approximation går mot en likhet i gränsvärdet.
Lol tusan, nu skrev jag att jag tänkte som dig fast din kommentar kom inte upp förrän jag refreshade sidan... men så enligt detta resonemanget så bör " min " lösning också vara rätt eller?
Hpakuten skrev:Lol tusan, nu skrev jag att jag tänkte som dig fast din kommentar kom inte upp förrän jag refreshade sidan... men så enligt detta resonemanget så bör " min " lösning också vara rätt eller?
Det spelar ingen roll hur du laborerar med uttrycket (till skillnad från det Henning skrev). Ett konvergerande gränsvärde kan du laborera med precis som om det vore en helt vanlig ekvation. Detta gör att din lösning är helt korrekt. Det är divergerande gränsvärden du måste vara försiktig med då laborering med dem kan producera en del nonsens.
Det du borde gjort är att tillämpa ditt resonemang direkt:
Här har du att i gränsvärdet så du får:
Om vi nu ska vända på steken lite här kan vi diskutera en situation som gör att de saker som tagits upp i tråden måste hanteras med varsamhet. Hpakuten, kan du beräkna följande gränsvärde:
Ebola skrev:Hpakuten skrev:Lol tusan, nu skrev jag att jag tänkte som dig fast din kommentar kom inte upp förrän jag refreshade sidan... men så enligt detta resonemanget så bör " min " lösning också vara rätt eller?
Det spelar ingen roll hur du laborerar med uttrycket (till skillnad från det Henning skrev). Ett konvergerande gränsvärde kan du laborera med precis som om det vore en helt vanlig ekvation. Detta gör att din lösning är helt korrekt. Det är divergerande gränsvärden du måste vara försiktig med då laborering med dem kan producera en del nonsens.
Det du borde gjort är att tillämpa ditt resonemang direkt:
Här har du att i gränsvärdet så du får:
Då fattar jag! Såg inte lösningen direkt när jag gjorde uppgiften så gick instinktivt över till ekvationslösning och isolerade A. Ser dock hur man ska tänka nu. Tack för all hjälp allihopa!
Ebola skrev:Om vi nu ska vända på steken lite här kan vi diskutera en situation som gör att de saker som tagits upp i tråden måste hanteras med varsamhet. Hpakuten, kan du beräkna följande gränsvärde:
Såg inte att du skrev förrän nu! Vid första ögonkast och det jag läst i denna tråden i åtanke vill jag säga att (1+1/x) kommer närma sig 1 ju större x blir, 1/x bör ju bli försumbart. Därför bör limx->inf(1+1/x)^x ge gränsvärdet 1 eftersom 1^x=1.
Om man sen kör en numerisk analys ( för o slänga in lite fancy pants ord :p tror det heter så iallafall? ) ser man dock att för x=10 blir värdet (1.1)^10 vilket blir bra mycket större än 1. Vidare ger x=100 (1+1/100)^100=(1.01)^100 som självklart också är större än 1, o x=10^3 ger (1.001)^1000 etc. Nu vet jag ju att man inte ska dra slutsatser ifrån så pass "små" x-värden vid beräkning av gränsvärden, men när jag läste om det originella problemet i OP på reddit nämnde någon någonting om att olika x dock kan närma sig oändligheten olika snabbt, och jag gissar på att det är det man ska tänka på här då? Så x i exponenten ökar snabbare än vad 1/x minskar...? Kanske? haha
Samtidigt tänker jag att det kanske finns någon algebra magi man kan använda för att lättare se svaret, typ genom någon förenkling? Vet inte ifall jag missar någon enkel detalj. Har stirrat på det i typ 40 minuter nu utan att komma någon vart. Tänker att det finns 2 möjligheter:
1. Gränsvärdet är 1 och jag bara försöker undvika en fälla som inte finns ( minst sannolik känner jag )
2. Gränsvärdet är oändligheten
Antingen blir gränsvärdet i parantesen 1, men eftersom du säger att det vi tagit upp här ska hanteras varsamt är det nog inte så enkelt. Om det inte är 1 måste det väl bli större och större allt med att x ökar, eftersom alla n>1 som skrivs på funktionen n^x går mot oändligheten då x växer. Så jag gissar på att gränsvärdet är oändligheten, men någon bestämning harjag ingen aning om hur man gör.
Kolla nu vad du gjort, klockan är 3 och jag känner mig dum. Som straff krävs du på en knuff i rätt riktning! :P
Hpakuten skrev:[Många bra tankar]
Jag tänker inte gå in på så många detaljer då det snabbt blir överkurs och jag är inte den bästa av pedagoger när det kommer till matematik. Enkelt sagt är du helt inne på rätt spår och det rätta svaret är nära ditt resonemang. Det kräver dock matematik på universitetsnivå att visa varför och jag lämnar det därhän.
Faktum är att gränsvärdet är det märkliga, transcendentala talet . Det som beskriver naturlig förändring och har oändligt många tillämpningar inom matematik. Vi kan se det genom att knappa in på miniräknaren. För får vi:
För får vi:
Som du ser närmar vi oss Eulers tal.
Jag önskar dig all lycka till med dina fortsatta studier. Om du håller fast i vetgirigheten kommer du lära dig mycket.
Ebola skrev:Hpakuten skrev:[Många bra tankar]
Jag tänker inte gå in på så många detaljer då det snabbt blir överkurs och jag är inte den bästa av pedagoger när det kommer till matematik. Enkelt sagt är du helt inne på rätt spår och det rätta svaret är nära ditt resonemang. Det kräver dock matematik på universitetsnivå att visa varför och jag lämnar det därhän.
Faktum är att gränsvärdet är det märkliga, transcendentala talet . Det som beskriver naturlig förändring och har oändligt många tillämpningar inom matematik. Vi kan se det genom att knappa in på miniräknaren. För får vi:
För får vi:
Som du ser närmar vi oss Eulers tal.
Jaha, se där! Hade aldrig gissat att det skulle bli det. Gick ändå och la mig den natten med känslan av att min gissning var korrekt haha. Men det där är ju riktigt konstigt. Känns som att mycket av det som har att göra med Eulers tal är riktigt skumt dock.
Jag önskar dig all lycka till med dina fortsatta studier. Om du håller fast i vetgirigheten kommer du lära dig mycket.
Tack! Det har varit en givande diskussion, har lärt mig massa jag inte hade lärt mig på egen hand. Det hade aldrig gått utan er på pluggakuten! :)



