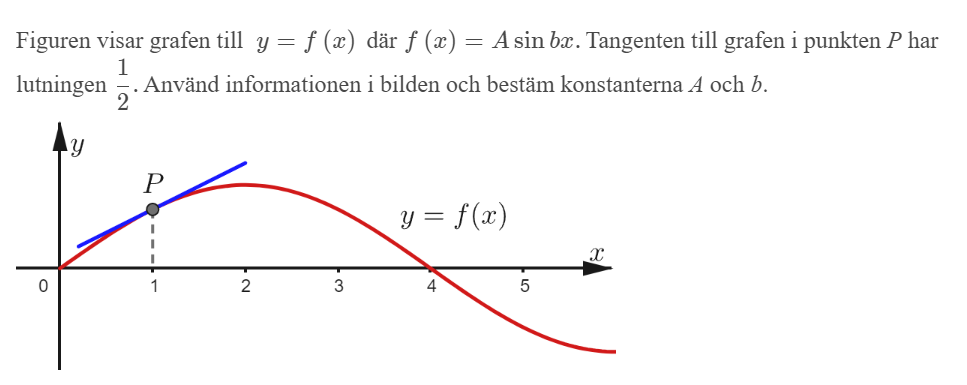
Bestäm konstanterna

Kan jag börja med att ta fram derivatan sinus

$D\left(\sin \right(x\left)\right)=\cos \left(x\right)$

Sen vet jag att P:s lutning ska bli $\frac{1}{2}$

Arup skrev:

Kan jag börja med att ta fram derivatan sinus

$D\left(\sin \right(x\left)\right)=\cos \left(x\right)$

Sen vet jag att P:s lutning ska bli $\frac{1}{2}$

Bra början

Arup skrev:

Kan jag börja med att ta fram derivatan sinus

$D\left(\sin \right(x\left)\right)=\cos \left(x\right)$

Ja, fast tänk på att f(x) är en sammansatt funktion, så att du får med inre derivatan.

Jag undrar var det så här man skulle derivera funktionen mha 

kedje-regeln =?

$$\begin{gathered} f\left(x\right)=A \sin \left(bx\right) \\ D\left(f\right(x\left)\right)=D(A\times \sin (bx\left)\right) \\ f\text{'}\left(x\right)=A\cos \left(bx\right)\times b \\ f\text{'}\left(x\right)=Ab\cos \left(bx\right) \end{gathered}$$

Ja.

För att ta mig vidare borde jag ställa 

$$\begin{gathered} f\text{'}\left(x\right)=\frac{1}{2} \\ Ab\cos \left(bx\right)=\frac{1}{2} ? \end{gathered}$$

Arup skrev:

För att ta mig vidare borde jag ställa 

$$\begin{gathered} f\text{'}\left(x\right)=\frac{1}{2} \\ Ab\cos \left(bx\right)=\frac{1}{2} ? \end{gathered}$$

Jag hade börjat med nollstället x=4 och bestämt b. Det blir enklare då.

Utifrån bilden har jag väl två nollställen. Dvs x₁=0 och x₂=4

x = 0 är alltid ett nollställe till Asin(bx), så det ger ingen information om b eller A.

Laguna skrev:

x = 0 är alltid ett nollställe till Asin(bx), så det ger ingen information om b eller A.

Jag förstår inte vad du menar. Varför skulle inte den andra nollstället dvs $x_2=0$ge mig någon information ?

Sätt in x = 0 och se vad du får.

Sin(bx)=0 för alla värden på b när x=0. Det ger dig inte någon information om b. 

Det är mer intressant att funktionen korsar x-axeln då x=4. Det säger någonting om b. 

Så här trodde jag man skulle göra

$$\begin{gathered} \sin \left(bx\right)=0 \\ {\sin }^{-1}\left(\sin \right(bx\left)\right)={\sin }^{-1}\left(o\right)+n*\mathrm{\pi } \\ \mathrm{bx}=\frac{\mathrm{\pi }}{2}+\mathrm{n}*\mathrm{\pi } \\ \mathrm{b}=\frac{\mathrm{\pi }}{2\mathrm{x}}+\mathrm{n}\times \mathrm{\pi } \end{gathered}$$

f(x)= Asin bx                                     (1)

f´(x)=Abcosbx (som visat ovan)  (2)

Ur sambandet (1) erhålles för sinusfunktionens första halvperiod (sin pi=0) att

b4=pi så b=pi/4

Ur sambandet (2) erhålles nu för x=1 och f´(1)=1/2 att 

1/2=A (pi/4) cos ((pi/4)*1) som ger A då cos (pi/4)=1/sqr(2)