Bestäm konstanterna a och b så att funktionen f blir deriverbar för alla x.

Att $f'$ är kontinuerlig $\forall x$ implicerar att $f$ är deriverbar. Och om $f$ är deriverbar kommer $f$ också vara kontinuerlig. 

Har du gjort uppgift 1 till 3? Hur ser de ut?

MrPotatohead skrev:

Att $f'$ är kontinuerlig $\forall x$ implicerar att $f$ är deriverbar.  

Nja, hur är det med den gröna funktionen som jag ritade? (Jag är inte matematiker...)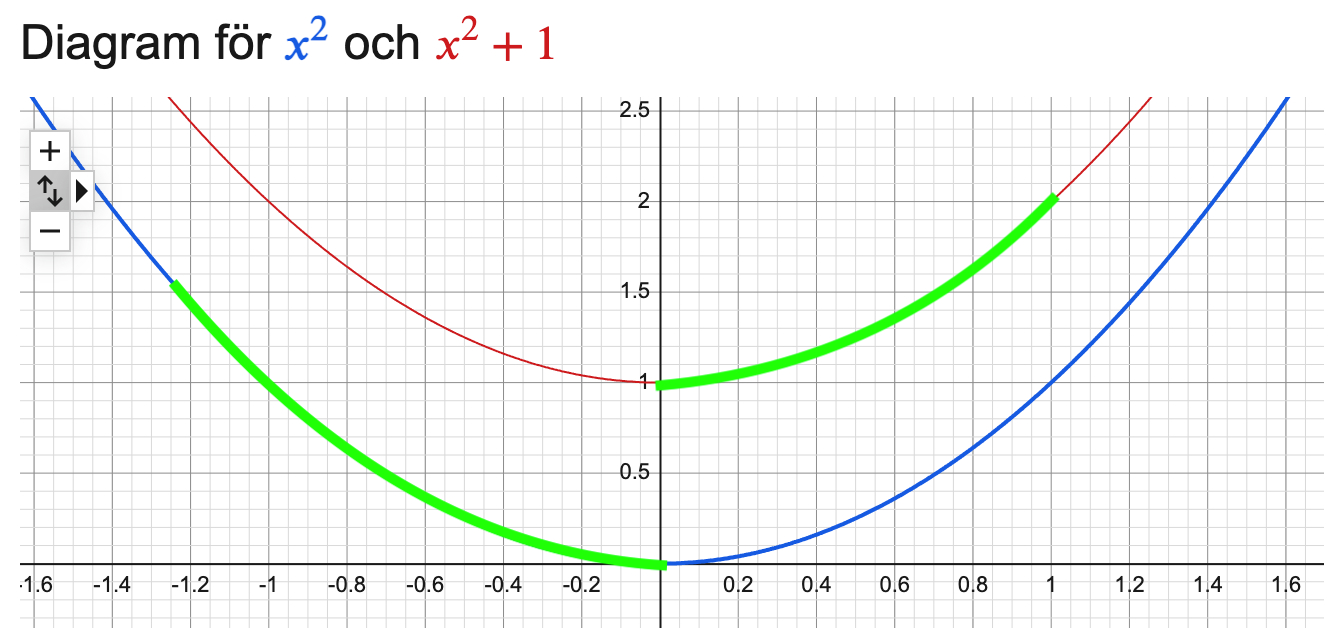

Jag är heller ingen matematiker men din funktion är inte kontinuerlig i 0 och kan således inte vara deriverbar där.

Tillägg: 12 maj 2025 18:31

Men något skaver så förhoppningsvis kommer en matematiker snart till undsättning, vilket jag mår dåligt över att säga. 

tack! cool zenitsu pfp btw

Om en funktion $f(x)$ är deriverbar i en punk $x=a$ så följer det precis som MrP skriver att $f(x)$ även är kontinuerlig i $x=a$. Bevisidé: Använd derivatans definition. 

@PK: Den gröna funktionen i #4 är inte deriverbar. Om vi applicerar derivatans definition i punkten $x=0$ kommer vi få gränsvärdet

$\lim_{h\to 0} \frac{f(h)-f(0)}{h}$

som inte existerar.