11 svar

684 visningar

Lisa Mårtensson behöver inte mer hjälp

Bestäm koordinaterna för vektorerna

Här kommer en uppgift som jag skulle behöva hjälp med att komma igång med. Var ska jag börja?

Så här lyder uppgiften:

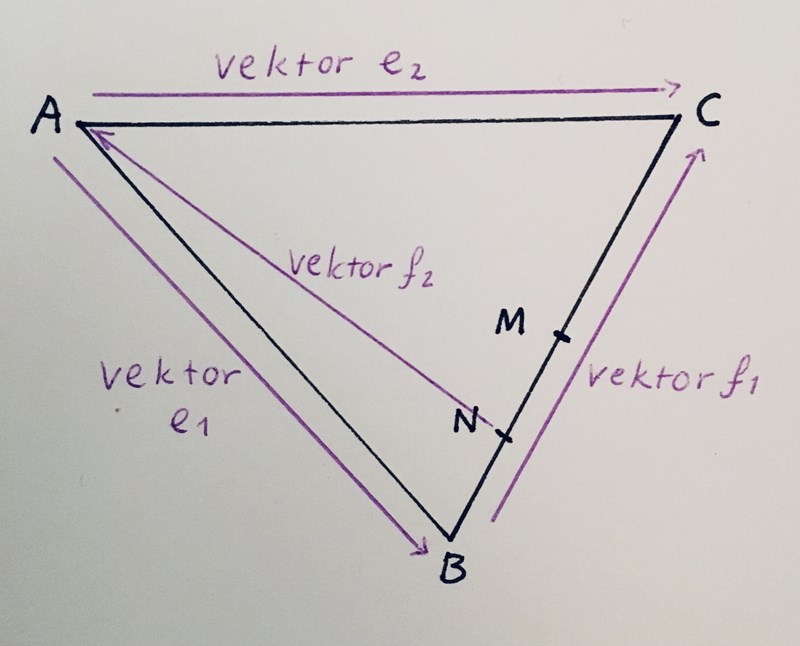
I triangeln $△ A B C,$ låt M vara mittpunkten på BC och N mittpunkten på BM. Då utgör vektorerna $\underset{e_{1}}{\to}$ $= \bar{A B}$ och $\underset{e_{2}}{\to}$ $= \bar{A C}$ en bas i planet. Bestäm koordinaterna för vektorerna $f_{1}$ $= \bar{B C}$ och $f_{2}$ $= \bar{A N}$ i denna bas. Uttryck även vektorerna $\underset{e_{1}}{\to}$ , $\underset{e_{2}}{\to}$ i basen $f_{1}, f_{2} .$

Börja med att rita.

Genom vektoraddition vet vi att

$A B + B C = A C ∥ ∥ ∥ e_{1} f_{1} e_{2}$

och att

$f_{2} = A B + \frac{1}{4} B C .$

Alltså är $\vec{f_{1}} = \vec{e_{2}} - \vec{e_{1}}$ och $\vec{f_{2}} = \vec{e_{1}} + \frac{1}{4} (\vec{e_{2}} - \vec{e_{1}})$ = $\frac{3}{4} \vec{e_{1}} + \frac{1}{4} \vec{e_{2}} .$

Detta ger koordinaterna i basen ( $\vec{e_{1}}, \vec{e_{2}}$ ).

Om jag löser ut $\vec{e_{1}}$ och $\vec{e_{2}}$ får jag svaret på andra delfrågan, dvs, hur jag ska uttrycka vektorerna i basen $f_{1}$ och $f_{2}$ .

Verkar jag vara rätt ute?

Jag tycker beräkningarna ser rätt ut hittills (däremot har du ritat vektor $f_2$ åt fel håll i din bild!).

En metod för att uttrycka $\vec{e_1}$ och $\vec{e_2}$ i basen $\{\vec{f_1},\vec{f_2}\}$ är ju att betrakta det hela som ett ekvationssystem:

$\vec{f_1}=\vec{e_2}-\vec{e_1}$

$\vec{f_2}=\dfrac{3}{4}\vec{e_1}+\dfrac{1}{4}\vec{e_2}$

där du vill lösa ut för $\vec{f_1}$ och $\vec{f_2}$ . Det finns dock lite genvägar. Exempelvis kan du ju inse geometriskt att

$\vec{e_1}=\vec{f_2}-\dfrac{1}{4}\vec{f_1}$

vilket gör det hela lite mindre beräkningstungt.

$\vec{e_{1}}$ har vi då löst ut och skrivit i basen $\vec{f_{1}}$ och $\vec{f_{2}}$ .

Om jag på samma sätt vill inse geometriskt vad $\vec{e_{2}}$ blir i basen $\vec{f_{1}}$ och $\vec{f_{2}}$ så är mitt förslag

$\vec{e_{2}}$ = $\vec{f_{2}} + \frac{3}{4} \vec{f_{1}}$ . EDIT: Jag har nu ändrat till $\vec{e_{2}}$ i VL.

Stämmer detta och behöver jag visa samma resultat genom att lösa ekvationssystemet för att få rätt på denna uppgift, tror ni?

Lisa Mårtensson skrev:
$\vec{e_{1}}$ har vi då löst ut och skrivit i basen $\vec{f_{1}}$ och $\vec{f_{2}}$ .
Om jag på samma sätt vill inse geometriskt vad $\vec{e_{2}}$ blir i basen $\vec{f_{1}}$ och $\vec{f_{2}}$ så är mitt förslag
$\vec{e_{1}}$ = $\vec{f_{2}} + \frac{3}{4} \vec{f_{1}}$ .
Stämmer detta och behöver jag visa samma resultat genom att lösa ekvationssystemet för att få rätt på denna uppgift, tror ni?

Ja, det stämmer, förutsatt att du menat att skriva $\vec{e_2}$ istället för $\vec{e_1}$ . :-)

Jag tycker geometriskt fungerar minst lika bra (om inte bättre) jämfört med att lösa det som ett ekvationssystem.

AlvinB skrev:
En metod för att uttrycka $\vec{e_1}$ och $\vec{e_2}$ i basen $\{\vec{f_1},\vec{f_2}\}$ är ju att betrakta det hela som ett ekvationssystem:
$\vec{f_1}=\vec{e_2}-\vec{e_1}$
$\vec{f_2}=\dfrac{3}{4}\vec{e_1}+\dfrac{1}{4}\vec{e_2}$
där du vill lösa ut för $\vec{f_1}$ och $\vec{f_2}$ .

Hur skulle man lösa detta ekvationssystem om man ändå ville göra det, trots att det inte är det enklaste sättet att lösa uppgiften?

Jag ser nu att jag skrev fel i mitt inlägg. Du skall såklart lösa ut för $\vec{e_1}$ och $\vec{e_2}$ .

Du kan ju exempelvis börja med att lösa ut $\vec{e_1}$ ur:

$\vec{f_1}=\vec{e_2}-\vec{e_1}$

och sedan sätta in i

$\vec{f_2}=\dfrac{3}{4}\vec{e_1}+\dfrac{1}{4}\vec{e_2}$

Ja, just det. Jag förstod nästan det.

Då har vi att

$\vec{e_{1}} = \vec{e_{2}} - \vec{f_{1}}$ .

Sedan sätter jag in uttrycket för $\vec{e_{1}}$ i uttrycket för vektorn ${\vec{f}}_{2} :$

$\vec{f_{2}} = \frac{3}{4} \cdot (\vec{e_{2}} - \vec{f_{1}}) + \frac{1}{4} \vec{e_{2}} .$

Vilket i sin tur ger att

$\vec{f_{2}} = \frac{3}{4} {\vec{e}}_{2} - \frac{3}{4} \vec{f_{1}} + \frac{1}{4} {\vec{e}}_{2}$

och slutligen har vi löst för ${\vec{e}}_{2}$ så att

$\vec{e_{2}} = {\vec{f}}_{2} + \frac{3}{4} {\vec{f}}_{1} .$

Hur gör man därefter för att bestämma koordinaterna.

Faja skrev:
Hur gör man därefter för att bestämma koordinaterna.

Hej och välkommen till Pluggakuten!

Du får snabbare och bättre svar om du startar en ny egen tråd med din fråga och visar hur långt du har kommit.

Svara

Visa senaste svar