Bestäm längden till kurvan. Behövs arcsin?
Hej!
Jag hade uppgift
Efter lite fumbling och slarv hittar jag lösningen 38/3. Men grejen är att jag blev förvirrad, kan eller borde man använda arcsin nån gång? Jag försökt applicera tumreglerna.
Mitt slarvigt men typ korrekt lösning:
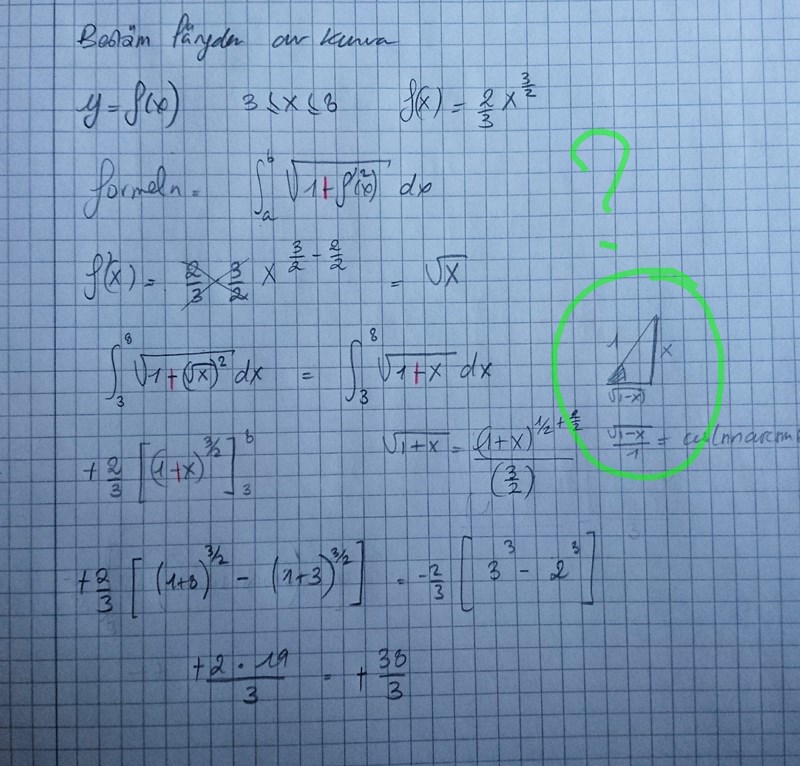
Om du har en linjär funktion under roten behöver man inte använda någon typ av trigonometrisk substitution. Då är det bara att göra en substitution och . Trigonometrisk substitution använder man när man har under roten.
Ok, förstår...
Jag är fortfarande urflippad? bizarrerad? (språkpolisen får gärna göra en insats här) av tecken.
Så vi skriver såhär:
, som betyder att vi trollar bort x i uttrycket t(eller??) innebär att som du säger...
Men när vi integrerar , vad händer till under integrationsprocess? Varför försvinner dem?
Vi gör ju bara ett helt normalt variabelbyte, och då byter vi mot eftersom vi nu integrerar med avseende på istället för .
Detta variabelbyte är ju dock så pass enkelt satt man inte alltid behöver göra hela och , utan man kan bara tänka att är en variabel som du gjort.
Men varför försvinner när vi integrerar? (Nu misstänker du säkert att jag sov min väg igenom matte 4...)
Vad menar du med "försvinner"? säger egentligen bara vilken variabel man ska integrera med avseende på. Har man ska man integrera med avseende på , har man ska man integrera med avseende på .
När man gör det här med är det egentligen bara för att tala om vad vi måste ta bort eller lägga till för att få byta variabel till och integrera med avseende på . Man ställer sig helt enkelt frågan "Vad behöver vi för att byta mot så vi kan integrera med avseende på ?".
Tack, polletter börjar att sätta sig.
Mitt problem är att det kändes att dx hade bara en dekorativ syfte i tidigare matte, men nu måste vi börja räkna med den, och jag är helt förvirrad. Men mindre nu, jag lovar att dina tråd går inte helt för Java.



