bestäm linje och plan? (Linj algebra)

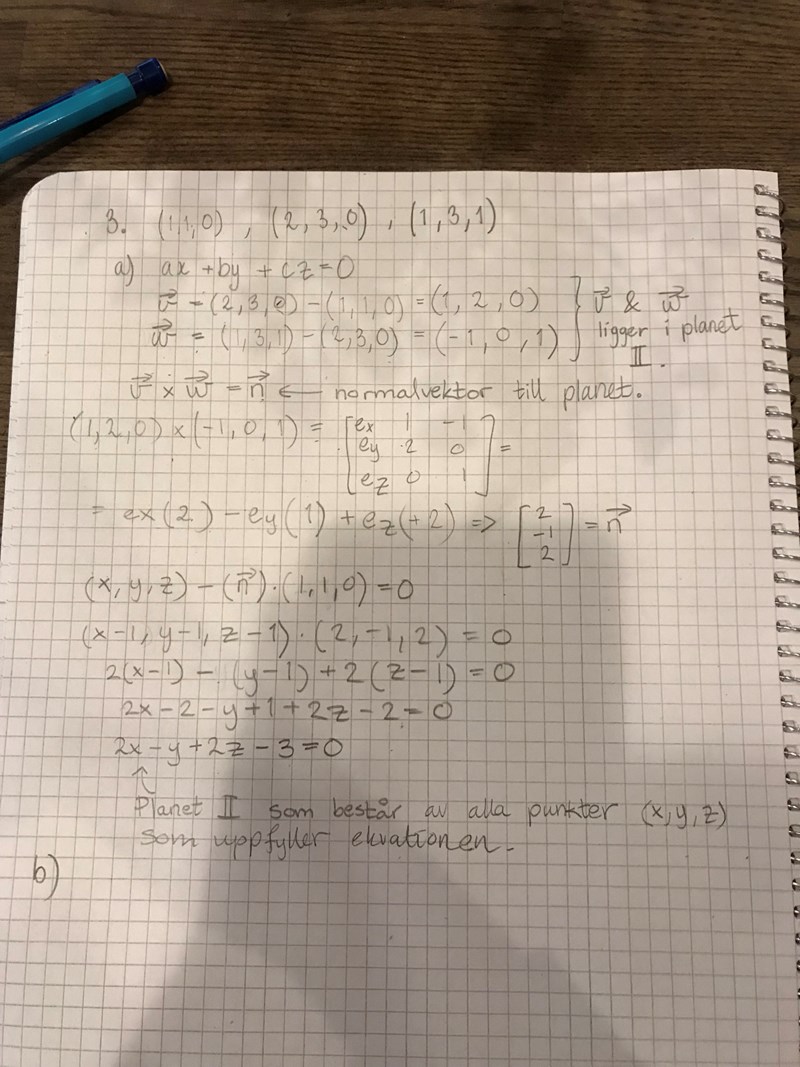 Har jag gjort rätt på a)? Och hur gör man b)?
Har jag gjort rätt på a)? Och hur gör man b)?
(Den första punkten skulle vara (1,0,0).)
Något har blivit fel, då ingen av de tre punkterna ligger i ditt uträknade plan.
Du vet att ax+by+cz+d=0 för alla punkter som ligger i planet. Du vet tre punkter som ligger i planet. Gör ett ekvationssystem och lös det. Lösningen kommer att innehålla en parameter (när jag räknade blev det a). Förläng med nånting lämpligt för att få bort den.
Jag skulle i detta fall föredra den vektoralgebraiska lösningen, som du är inne på. Dock ritar jag vektorerna v och w med gemensam fotpunkt, enligt denna figur:

Vektorn resp. .
Normalvektorn (som även är linjen L:s riktningsvektor)
Med punkten , godtyckligt vald i planet, skriver vi planets ekvation
, dvs planets ekvation är .
Uppgift (b): Linjen L:s ekvation. , där och är punkter på L, Q godtyckligt vald.
Nu tror jag du kan fortsätta på egen hand, även med Uppg (c).




