Bestäm matris för linjär avbildning ?
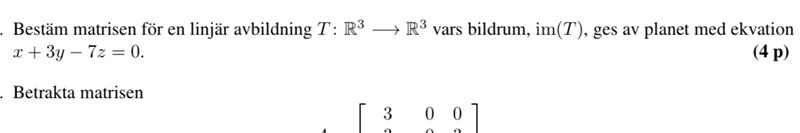 jag har svårt att hänga med på hur man ska föreställa det här och förstår fortfarande inte helt vad im(T) är för något (det ska tydligen vara samma som värdemängd men hänger inte riktigt med hur jag ska liksom räkna på det). Hur får man ut en linjär avbildning baserat på ett plans bildrum?
jag har svårt att hänga med på hur man ska föreställa det här och förstår fortfarande inte helt vad im(T) är för något (det ska tydligen vara samma som värdemängd men hänger inte riktigt med hur jag ska liksom räkna på det). Hur får man ut en linjär avbildning baserat på ett plans bildrum?
facit tog bara ut några vektorer på linjen som inte var parallella och radade upp dessa i en matris men hänger inte alls med vad detta innebär och hur det hörs ihop med frågan!
Ja det stämmer att bildrummet är som värdemängd; en vektors som avbildas enligt T kommer hamna i im(T), dvs för alla .
Utifrån detta kan vi nog vara överens om att om man bara får reda på att bildrummet är ett plan så är det inte entydigt vilken avbildning man menar. Om T projicerar alla vektorer på planet så kommer im(T) vara planet, men om T först projicerar alla vektorer på planet och sedan roterar dem säg radianer runt en vektor som är normal mot planet kommer det ge samma bildrum: i båda fallen kommer alla resultat av avbildningen vara en vektor i planet, dvs planet är T:s bildrum.
Nästa steg är då hur vi ska använda informationen om bildrummet. Man kanske kan ta det på olika håll, men vet du exempelvis om att man med avbildningsmatrisens kolonner kan hitta en bas för bildrummet? Om du vet det kanske det kan vägleda?
Man antar säkert att R3s basvektorer är 100 010 och 001
Det där planet spänns upp av vektorerna , så avbildningsmatrisen är .
Jag kan inte redigera mitt inlägg längre men det var fel, jag gör det igen.
Planet spänns upp av Så då är avbildningsmatrisen de tre men i en matris. Sådär nu blev det rätt. Den tredje kan då vara vad som helst, bara det är en l.komb av de föregående två så att dim(col(a))=2.
Bump? Kam nån bekräfta att mitt svar är rätt?
Som jag skrev tidigare så är avbildningsmatrisen inte entydig med den information vi har. I båda dina svar har du angett baser för planet, vilket är vad som krävs och du har därför gett två möjliga korrekta svar.
Hondel skrev:Som jag skrev tidigare så är avbildningsmatrisen inte entydig med den information vi har. I båda dina svar har du angett baser för planet, vilket är vad som krävs och du har därför gett två möjliga korrekta svar.
Jag håller med dig om att det finns oändligt många tänkbara avbildningsmatriser med den efterfrågade egenskapen. Däremot skulle jag vilja påstå att Qetsiyah har helt rätt i att det blev lite fel i det första svaret, men rätt i det andra. Vektorerna och bildar en bas för planet ifråga (de spänner upp det och är linjärt oberoende), medan vektorerna och ju inte ens ligger i planet!
Man kan koka ihop fler tänkbara avbildningsmatriser genom att låta matrisens kolumner vara valfria linjärkombinationer av och , så länge inte alla linjärkombinationerna är multiplar av en och samma vektor.
Exempelvis kan vi ta , och , vilket ger matrisen
eller , och , vilket ger
Men det är alltså val av olika basvektorer för R3 som skapar olika lösningar?
Typ. I praktiken kan man kanske se det som man gör tre stycken val:
- Välj en bas för planet.
- Välj en linjärkombination för .
- Välj vilken av vektorerna som ska vara första, andra respektive tredje kolumnen i .
Ah just det, 2. 3. tänkte jag inte på. Men 1. avgörs av vårt val av basvektorer för R3?
Finns det något som kallas "kolonnekvivalent"?
Hm, jag läste din fråga slarvigt ser jag nu. Vad menar du att det är för bas för som vi väljer?
När det gäller kolumnekvivalens, så skulle man absolut kunna införa ett sådant begrepp!
Mer precist skulle vi kunna säga att två matriser är kolumnekvivalenta om . Detta ger en så kallad ekvivalensrelation på mängden , och som alltid när man har ekvivalensrelationer kan man fundera på vad som händer om man identifierar alla ekvivalenta element med varandra (vilket formellt innebär att vi tittar på mängden av så kallade ekvivalensklasser).
Detta är särskilt intressant om vi begränsar oss till fallet samt enbart betraktar matriser av rang . Om vi då genomför den här identifikationen så får vi en konkret (nåja) "inkarnation" av den så kallade Grassmannianen (mängden av alla -dimensionella underrum i , som är ett väldigt centralt objekt i både differentialgeometri och algebraisk geometri).
Den här "inkarnationen" är faktiskt precis vad man brukar ha i åtanke när man definierar vad man menar med en öppen delmängd i (man behöver ett öppenhetsbegrepp för att kunna prata om saker som kompakthet och kontinuerliga funktioner till och från Grassmannianen). Man säger helt enkelt att en mängd (som alltså är en mängd av underrum i , vilket kanske är lite förvirrande första gången man stöter på det) är öppen om och endast om mängden är öppen i (med avseende på den vanliga topologin, som i sin tur erhålls genom att se matriser i som element i ).
Jag vet inte om det säger dig något (mer än att du kanske får ännu fler ord att kolla på Wikipedia nu :P ), men poängen är att det finns ett hyfsat meningsfullt/användbart "kolumnekvivalens"-begrepp där ute (även om man nog inte brukar ha något särskilt ord för det)!
oggih skrev:Hm, jag läste din fråga slarvigt ser jag nu. Vad menar du att det är för bas för som vi väljer?
Öh ja... ja att vi inte vet vilken bas R3 har i uppgiften?
Vektorer ändras ju också om man ändrar bas, så då trodde jag att plan också gör det.
Jag tolkar det som att allt är med avseende på standardbasen, dvs. att
att planet ges av
och att vi vill hitta en matris sådan att avbildningen med har som bild.



