Bestäm matriser X

Ge X några element, multiplicera med de, du får ett ekvationssystem, vips färdigt!

I facit står det att svaret är x=[7 -1 3]

Jag vet inte hur de har kommit fram till det. 

Ett alternativt sätt (som kan bli mer krånglig, men som är bra att veta existerar) är att multiplicera med $A^{T}$ från höger. Då får du en kvadratisk matris $AA^{T}$ som du sen (förhoppningsvis) kan invertera för att få lösningen $X=B\left(AA^{T}\right)^{-1}$.

EDIT: Det ska såklart vara $X=BA^{T}\left(AA^{T}\right)^{-1}$.

Moffen skrev:

Ett alternativt sätt (som kan bli mer krånglig, men som är bra att veta existerar) är att multiplicera med $A^{T}$ från höger. Då får du en kvadratisk matris $AA^{T}$ som du sen (förhoppningsvis) kan invertera för att få lösningen $X=B\left(AA^{T}\right)^{-1}$.

Jo det verkar vara ännu mer krångligt. Hur kan jag fortsätta med ekvationen som jag har påbörjat nu? 

Du kan skriva upp totalmatrisen och gausseliminera (om ni kommit så långt). Annars kan du testa att addera $5\cdot R_{2}$ till $R_{1}$ (rad 1 och rad 2).

Det blir fel svar när jag använder gauss elimination.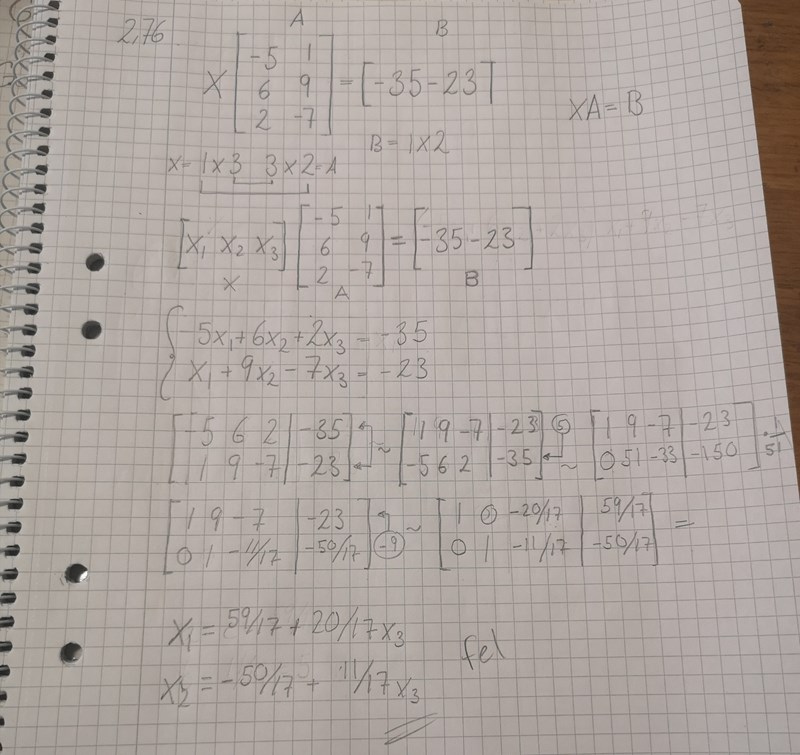

Hej Dilan,

Transponera ekvationen för att få den på välbekant form.

    $xA=b \iff A^{t}x^{t}=b^{t}$

där

    $x^{t} = \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}$ och $A^{t} = \begin{pmatrix}-5&6&2\\1&9&-7\end{pmatrix}$

samt

    $b^{t} = \begin{pmatrix}-35\\-23\end{pmatrix}.$

Sedan utför du gausselimination på den utökade koefficientmatrisen $(A^{t}|b^{t})$, det vill säga LU-faktorisering av matrisen $A^t.$

Det ser korrekt ut.

Notera att valet $x_{3}=3$ ger dig $x_{1}=7, x_{2}=-1$ men du har även hittat fler lösningar som beror på parametern $x_{3}$. Dvs. det finns inte bara en matris $X$ som uppfyller ekvationen utan oändligt många (för något val av värde på $x_{3}$.

Om du tycker att det är jobbigt med bråken så kan du även skriva om det som $17x_{1}=59+20x_{3}$ och på samma sätt för $x_{2}=...$.

Men hur får du fram att x3=3 och x2, x3... ?? 

$\begin{pmatrix}-5&6&2&|&-35\\1&9&-7&|&-23\end{pmatrix} \sim \begin{pmatrix}0&1&-\frac{11}{17}&|&-\frac{50}{17}\\1&9&-7&|&-23\end{pmatrix}$

Kolumnerna 1 och 2 är pivotkolonner vilket indikerar att den tredje variabeln $x_3$ är fri att variera och är därför en parameter ($s$) som de övriga två variablerna $x_1$ och $x_2$ kan uttryckas med. 

    $17x_2 = -50 + 11s$ vilket i sin tur ger $17x_1=59 + 20s$.

Sammanfattningsvis utgörs lösningsmängden av en rät linje i rummet: linjen går genom punkten $(1/17)(59,-50,0)^{t}$ och har riktningsvektorn $(20,11,1)^{t}.$

    $x^{t} = \frac{1}{17}\begin{pmatrix}59\\-50\\0\end{pmatrix}+u\begin{pmatrix}20\\11\\1\end{pmatrix}$ där parametern u = s/17.

Nu hänger jag med, tack så mycket!