Bestäm min och max (Optimisera DarthKnäckebröd)
Så nu frågan lyder:
Fråga 1:
Jag har räknat som vanligt. Undersökt rander av cirkeln med radie , och cirkel med randen .
Efter det har jag tittat på .
Men jag undrar en sak, jag får min maxvärde från den parametriserade funktion när jag sätter in värderna .
Men jag får exakt samma värde från , när ?
Jag kommer ihåg att ni sa för att det var därför att... något derivata var lika med noll.... Jag kommer inte ihåg.
Alltså om jag måste hitta samma svar från två olika hål, jag vill gärna förstå varför, för att undvika onödiga beräkningar.
Fråga 2:
Jag har detta kod för lösningen, fritt copypastad/modifierad från Guggles.
Clear[f, x, y, A, B, R, S]
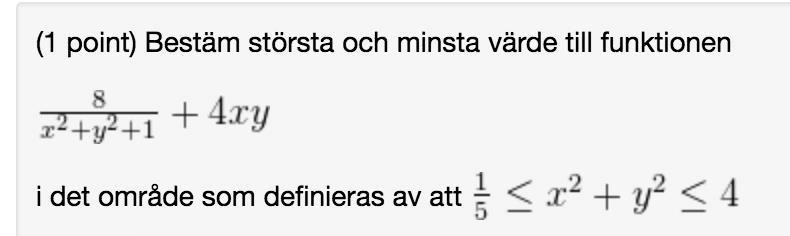
f[x_, y_] := (8/(x^2 + y^2 + 1)) + 4 x*y;
R = ImplicitRegion[{0.2 <= x^2 + y^2 <= 4}, {x, y}];
A = FindMaximum[{f[x, y], {x, y} \[Element] R}, {x, y}]
B = FindMinimum[{f[x, y], {x, y} \[Element] R}, {x, y}]
Minimize[{f[x, y], x^2 + y^2 == 4}, {x, y}]
Minimize[{f[x, y], x^2 + y^2 == 0.2}, {x, y}]
Plot3D[f[x, y], {x, y} \[Element] R,
ColorFunction -> (ColorData["Temperature"][#3] &)]
CirclePoints[A, B]
PlotMarkers[A, B]
Jag försöker använda temperaturen för att hitta min och max värde. Hur sätter man en pil som visar snällt var min punkt ligger?
Försökt : CirclePoints[A, B], och PlotMarkers[A, B], och Show... men det inte är rätt kommando.
Fråga 3, stilfråga:
Om jag vill ha en DarthKnackebröd som Guggles, vilket kod ska jag använda?
Min lösning: (som jag fotade bara för att säga att jag har gjort uppgiften med mina egna händer...)
(jo, ni får säga att detta förklara mitt otroligt antal slarvfel...)
.jpg?width=800&upscale=false)
dajamanté skrev:
Men jag undrar en sak, jag får min maxvärde från den parametriserade funktion när jag sätter in värderna .
Men jag får exakt samma värde från , när ?
De enda extrempunkterna som ligger inom intervallet är och . Jag vet inte var du får ifrån.
Sedan undrar jag även varför du skriver att (med antagandet att du råkat skriva istället för )
Du har ju redan satt in i och , och alltså skulle detta inte gälla för
En sista sak du kan kika på är följande:
Är du säker på att detta stämmer?
AlvinB skrev:dajamanté skrev:Men jag undrar en sak, jag får min maxvärde från den parametriserade funktion när jag sätter in värderna .
Men jag får exakt samma värde från , när ?
De enda extrempunkterna som ligger inom intervallet är och . Jag vet inte var du får ifrån.
Slarvfel såklart. Jag råkade skriva/räkna fel
Ok, men detta besvara frågan. Det var inga punkter som råkade ge samma resultat, eller hur?
Sedan undrar jag även varför du skriver att (med antagandet att du råkat skriva istället för )
Du har ju redan satt in i och , och alltså skulle detta inte gälla för
Jag tror jag räknade med också (ser jag på mitt äckligt papper (jag ser en svagt ) och diskalifierat reslutat som möjligt maximi och minimipunkt.
En sista sak du kan kika på är följande:
Är du säker på att detta stämmer?
Jag skrev gul, jag ska titta om jag slarvade annanståns.
Hej Daja,
Mathematicas funktioner Maximize[] och Minimize[] försöker hitta en funktions största- och minsta värde. Om funktionen och villkoren är snälla (t.ex. linjärt sluten definitionsmängd eller villkor givna av polynom) kommer man alltid hitta en global max- eller minpunkt.
Om funktionen får exakt indata försöker den ge dig ett exakt svar. Om det finns flera punkter som ger samma min- eller maxvärde kommer den fortfarande bara ge dig en punkt .
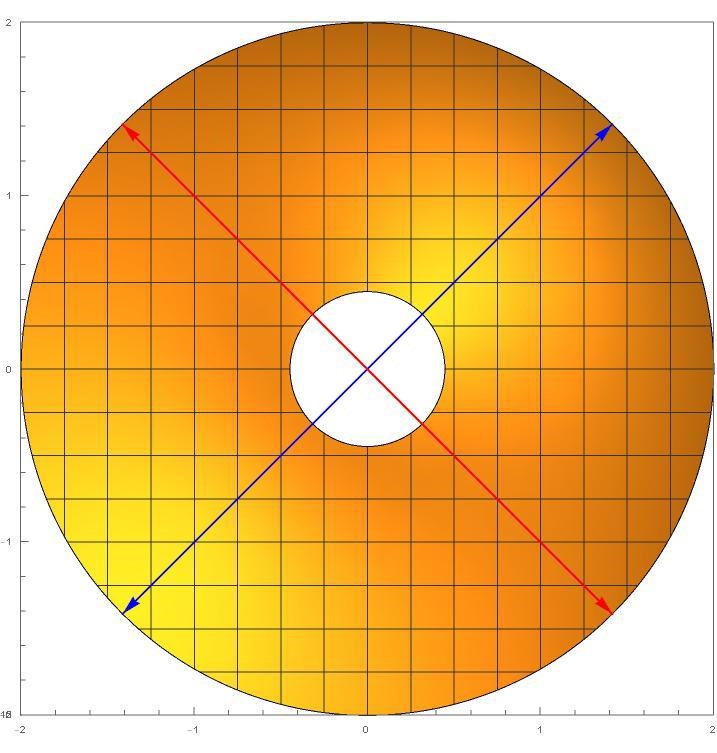
Den här koden ger dig funktionens max- och minvärde och pekar ut en maxpunkt och en minpunkt med två vackra pilar (de fyra första raderna hittar max och min, resten är att rita graf och pilar):
f[x_, y_] := 8/(x^2 + y^2 + 1) + 4*x*y;
R = ImplicitRegion[1/5 <= x^2 + y^2 <= 4, {x, y}];
minpoint = Minimize[f[x, y], {x, y} \[Element] R, {x, y}]
maxpoint = Maximize [f[x, y], {x, y} \[Element] R, {x, y}]
Show[Plot3D[f[x, y], {x, y} \[Element] R,
PlotRange -> {{-2, 2}, {-2, 2}, {-7, 15}}, BoxRatios -> {2, 2, 1},
AspectRatio -> Automatic, ViewPoint -> {-3.2, 1.2, 0.4} ],
Graphics3D[{Blue, Arrowheads[Large],
Arrow[{{0, 0, 15}, {x, y, z} /.
Join[minpoint[[2]], {z -> minpoint[[1]] }]} ],
Arrow[{{0, 0, 15}, {x, y, z} /.
Join[maxpoint[[2]], {z -> maxpoint[[1]] }]} ]}]]
Det är alltså viktigt att förstå att funktionen antar såväl max-, som minvärde i 2 olika punkter vardera på randen. Av symmetri kommer maxpunkterna ligga på randen (r=2) på den blå linjen $$x=y$. Minpunkterna ligger på randen (r=2), på den röda linjen $$x=-y$$
Guggle skrev:Hej Daja,
Mathematicas funktioner Maximize[] och Minimize[] försöker hitta en funktions största- och minsta värde. Om funktionen och villkoren är snälla (t.ex. linjärt sluten definitionsmängd eller villkor givna av polynom) kommer man alltid hitta en global max- eller minpunkt.
Om funktionen får exakt indata försöker den ge dig ett exakt svar. Om det finns flera punkter som ger samma min- eller maxvärde kommer den fortfarande bara ge dig en punkt .
Tack så himla mycket!
Jo, våra lärarna säger alltid att man måste vara observant med mathematica, hon ger sina maskinsvar och vi måste ställa rätt fråga. Eller nåt sånt.
Den här koden ger dig funktionens max- och minvärde och pekar ut en maxpunkt och en minpunkt med två vackra pilar (de fyra första raderna hittar max och min, resten är att rita graf och pilar):
f[x_, y_] := 8/(x^2 + y^2 + 1) + 4*x*y;
R = ImplicitRegion[1/5 <= x^2 + y^2 <= 4, {x, y}];
minpoint = Minimize[f[x, y], {x, y} \[Element] R, {x, y}]
maxpoint = Maximize [f[x, y], {x, y} \[Element] R, {x, y}]
Show[Plot3D[f[x, y], {x, y} \[Element] R,
PlotRange -> {{-2, 2}, {-2, 2}, {-7, 15}}, BoxRatios -> {2, 2, 1},
AspectRatio -> Automatic, ViewPoint -> {-3.2, 1.2, 0.4} ],
Graphics3D[{Blue, Arrowheads[Large],
Arrow[{{0, 0, 15}, {x, y, z} /.
Join[minpoint[[2]], {z -> minpoint[[1]] }]} ],
Arrow[{{0, 0, 15}, {x, y, z} /.
Join[maxpoint[[2]], {z -> maxpoint[[1]] }]} ]}]]
I din gammelkod körde du NMinimise och NMaximize men jag har bytt till exakta värde för att vi måste skriva våra svar i exakta värderna.
Det är alltså viktigt att förstå att funktionen antar såväl max-, som minvärde i 2 olika punkter vardera på randen. Av symmetri kommer maxpunkterna ligga på randen (r=2) på den blå linjen $$x=y$. Minpunkterna ligger på randen (r=2), på den röda linjen $$x=-y$$
Mycket vackert knackebröd! Vilket färgkod använder du för din Darth Dal? (den grå bild!)
dajamanté skrev:I din gammelkod körde du NMinimise och NMaximize men jag har bytt till exakta värde för att vi måste skriva våra svar i exakta värderna.
Ja, alla funktioner som heter N i förnamn är Numeriska. Om Maximize tar för lång tid att exekvera kan du alltid använda NMaximize istället.
Mathematica är oerhört kraftfull, men hon gör bara det man säger åt henne. För att förstå vilka begränsningar och fallgropar som finns bör man ha läst en kurs i numerisk analys, något om brukar komma i årskurs två eller tre. Men det går för det mesta bra att läsa en introduktionskurs och använda sunt förnuft :)
Mycket vackert knackebröd! Vilket färgkod använder du för din Darth Dal? (den grå bild!)
Om du menar bilden med grå-grön-blå färgskala så kommer den från Mathematicas pojkvän Matlab och blir svår att återskapa exakt.
Men du vet väl att du kan använda Texture[] och vilken bild som helst för att täcka dina funktionsytor? Här är din funktion med en logga från ett känt Forum, bonuspoäng om du kan räkna ut vilket!
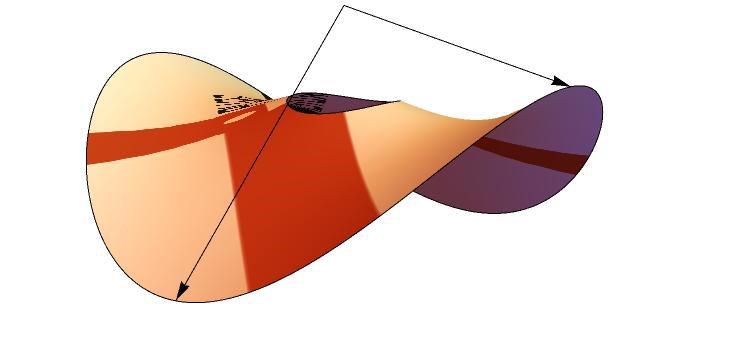
Dajas funktion med max och minpunkter
Jag ber om ursäkt att svara så sent, det blev väldigt busy Midsommar, c++ och sånt.
Jag får inte till det!
Jag har testat med Plotstyle->Texture (i insidan av parentesen Graphic3D och i Plot3D...), men det ser ut som man måste lägga en liten bild mellan []? Efter testade jag med ExempelData (spara en bild som img och Texture[img]), det blev inte bättre.
Jag importerade PA bilden och sånt (eller måste jag lägga den i library?), jag bara lyckades bryta sönder knackebrödet:





