Bestäm minsta värdet

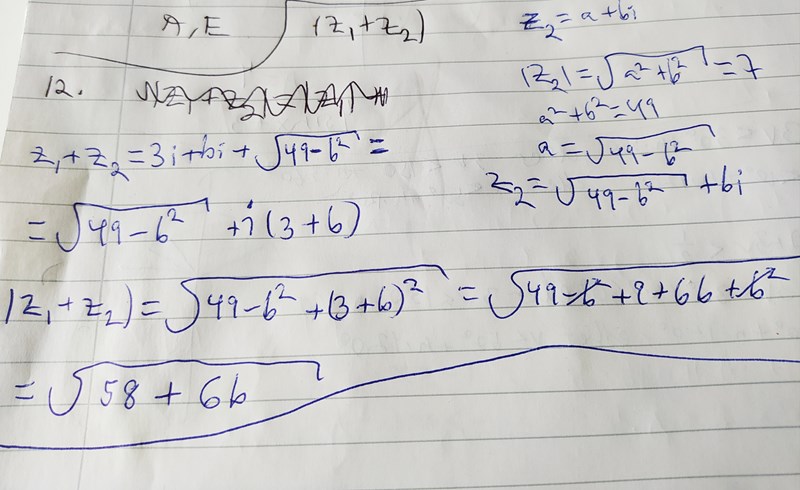
Var blir det fel i min lösning. Löser jag den där får jag ju att det kan vara 0 men det stämmer ju inte.
Tacksam för hjälp!!
Du kan inte välja b hursomhelst.
Du har kravet att a2 + b2 = 49, så vi måste ha att |b| 7.
Jag tror att det är lättare att fundera kring talen geometriskt – nu måste du oroa dig för rotuttryck och minustecken. Var i det komplexa talplanet kan ett tal med absolutbelopp 7 ligga? :)
Jag tycker du gör rätt... Får tänka själv.
Om ritar upp alla möjliga värden på z2 så får man en cirkel med radien 7 med centrum i origo. z1 befinner sig då på y-värdet 3, på y-axeln.
Skall man minimera |z1 + z2| kan man se det som att man skall hitta det värde på z2 som gör att avståndet mellan z1 och -z2 blir så litet som möjligt. Har vi hittat -z2 så har vi även hittat z2. Vilken punkt på denna cirkel av potentiella värden ligger längst från z1?
Jag vill få det att det blir -z2= i*7, vilket gör att z2= -i*7.
Tack jag förstår nu när jag gör geometriskt istället! :D



