Bestäm nollrum och bildrum?
Hej
Kan man bestämma mha determinaten istället för gaus eliminering?
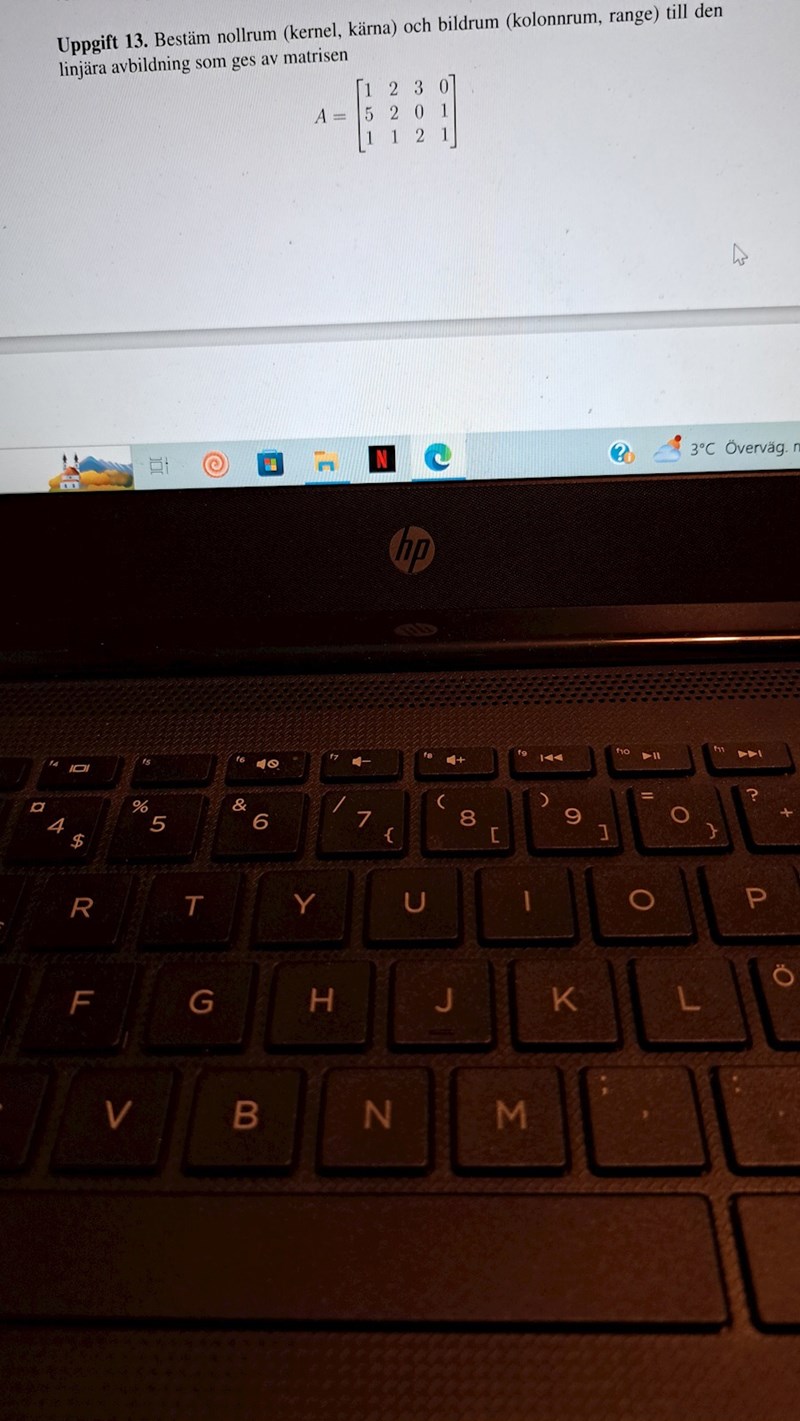
En determinant kräver att matrisen kvadratisk
Mogens skrev:En determinant kräver att matrisen kvadratisk
Ja juste! Provade med gaus eliminering men jag kommer endast fram till denna
1 0 5 2
00 1 1
0 -1 11
Sorry, jag har inte detta aktuellt, men elimineringen verkar inte färdig.
Mogens skrev:Sorry, jag har inte detta aktuellt, men elimineringen verkar inte färdig.
Ja jag vet jag började om från början
Får denna matris nu...

OK, har inte kollat men ser rimligt ut. Tänk på följande
AX = Y
Det är alltså en funktion från R^4 till R^3. Nollrummet är en delmängd av R^4, bildrummet en delmängd av R^3.
Nollrummet är de X som A avbildar på Y = 0
Bildrummet är de olika Y som förekommer som bilder av alla olika X.
Nollrummet ges alltså av
x+ +3u = 0
y+ +13u = 0
z 7u = 0
Om du sätter u = t så kan du skriva
x = –3t
y = –13t
z = –7t
u = t
vilket gör det lätt att skriva nollrumsvektorn på parameterform.
När det gäller bildrummet så är de tre första kolumnerna i den eliminerade matrisen just basvektorerna i R^3 så bildrummet är hela R^3.
Mogens skrev:Nollrummet ges alltså av
x+ +3u = 0
y+ +13u = 0
z 7u = 0
Om du sätter u = t så kan du skriva
x = –3t
y = –13t
z = –7t
u = t
vilket gör det lätt att skriva nollrumsvektorn på parameterform.
När det gäller bildrummet så är de tre första kolumnerna i den eliminerade matrisen just basvektorerna i R^3 så bildrummet är hela R^3.
Jag gausade fel och löste problemet. Tack!!

