Bestäm ortogonal projektion

Löste den på följande sätt

Ställde typ samma fråga härmodagen:

https://www.pluggakuten.se/trad/bestam-avbildningsmatrisen-4/ 

Etthejfrånpolhem skrev:

Löste den på följande sätt

Ställde typ samma fråga härmodagen:

https://www.pluggakuten.se/trad/bestam-avbildningsmatrisen-4/ 

Dum fråga, men jag förstår inte hur man multiplicerar matriserna till att få en 3x3 matris...

Finns det något annat sätt att lösa uppgiften på? Även om jag läst de andra trådarna så förstår jag inte riktigt helt 

Det finns många sätt. Men jag tänker att vi börjar med att utgå från ditt eget försök.

Linjen i uppgiften går genom origo, du behöver alltså inte lägga till någon punkt  $(x_1,x_2,x_3)$ i din lösning. Jag tror också du blandar ihop projektion på linje med projektion på ett plan.

För att projicera en vektor på en annan vektor kan man använda något som kallas projektionsformeln:

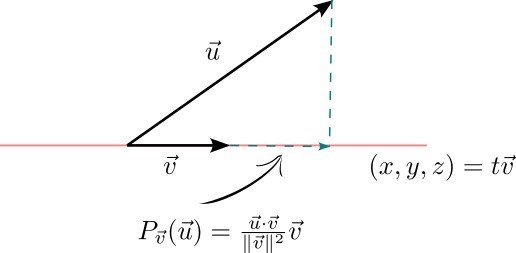
I den här bilden ska det röda föreställa linjen $t(1,1,1)$ genom origo och vektorn, $\vec{u}$ är vektorn du vill projicera på linjen.  Den grönaktiga horisontella vektorn utmed linjen ska föreställa projektionen av vektorn $\vec{u}$ på vektorn $\vec{v}$.

Beteckningen $P_{\vec{v}}(\vec{u})$ betyder bara projektionen av $\vec{u}$ på $\vec{v}$. Försök hitta något liknande i din lärobok eller bland dina föreläsningsanteckningar.

För att hitta avbildningsmatrisen  T kan man sedan avbilda enhetsvektorerna ($\mathbf{e_1},\mathbf{e_2},\mathbf{e_3}$) i tur och ordning på riktningsvektorn $\vec{v}=(1,1,1)$ för linjen.

Den första kolonnen i T är då $P_v(\mathbf{e_1})=\frac13(1,1,1)$

Den andra kolonnen i T är då $P_v(\mathbf{e_2})$ osv.

Gör ett försök! Och glöm inte att skissa en egen bild över projektionen.

D4NIEL skrev:

Det finns många sätt. Men jag tänker att vi börjar med att utgå från ditt eget försök.

Linjen i uppgiften går genom origo, du behöver alltså inte lägga till någon punkt  $(x_1,x_2,x_3)$ i din lösning. Jag tror också du blandar ihop projektion på linje med projektion på ett plan.

För att projicera en vektor på en annan vektor kan man använda något som kallas projektionsformeln:

I den här bilden ska det röda föreställa linjen $t(1,1,1)$ genom origo och vektorn, $\vec{u}$ är vektorn du vill projicera på linjen.  Den grönaktiga horisontella vektorn utmed linjen ska föreställa projektionen av vektorn $\vec{u}$ på vektorn $\vec{v}$.

Beteckningen $P_{\vec{v}}(\vec{u})$ betyder bara projektionen av $\vec{u}$ på $\vec{v}$. Försök hitta något liknande i din lärobok eller bland dina föreläsningsanteckningar.

För att hitta avbildningsmatrisen  T kan man sedan avbilda enhetsvektorerna ($\mathbf{e_1},\mathbf{e_2},\mathbf{e_3}$) i tur och ordning på riktningsvektorn $\vec{v}=(1,1,1)$ för linjen.

Den första kolonnen i T är då $P_v(\mathbf{e_1})=\frac13(1,1,1)$

Den andra kolonnen i T är då $P_v(\mathbf{e_2})$ osv.

Gör ett försök! Och glöm inte att skissa en egen bild över projektionen.

Jag hänger typ med. Har skisssat upp det och skrivit enligt beteckningarna som vi använder. Förstår bara inte hur jag får ||e||². 

Enhetsvektorerna är 1 långa så $\|\mathbf{e}\|=1$.

Men det du ska dela med i projektionsformeln är längden av riktningsvektorn för linjen i kvadrat, dvs längden av vektorn $\vec{v}=(1,1,1)$

Och den längden blir $\|(1,1,1)\|^2=1^2+1^2+1^2=3$. Det betyder $\|\vec{v}\|^2=3$

Visa gärna hur du räknat så kanske vi kan klura ut varför du fick $\|e\|^2$

D4NIEL skrev:

Enhetsvektorerna är 1 långa så $\|\mathbf{e}\|=1$.

Men det du ska dela med i projektionsformeln är längden av riktningsvektorn för linjen i kvadrat, dvs längden av vektorn $\vec{v}=(1,1,1)$

Och den längden blir $\|(1,1,1)\|^2=1^2+1^2+1^2=3$

Visa gärna hur du räknat så kanske vi kan klura ut varför du fick $\|e\|^2$

Glömde såklart klistra in bilden 

Du har med vektorn "två gånger". Därför kvadreras normen.

Det är bra om du väljer namn så att det framgår att vektorn är normerad. T.ex. kan du kalla den normerade vektorn $\hat{e}$ och den onormerade vektorn $\bar{e}$. Då är din formel

$\displaystyle \bar{u}^\prime=(\bar{u}\cdot \hat{e})\hat{e}=(\bar{u}\cdot \frac{\bar{e}}{\|\bar{e}\|})\frac{\bar{e}}{\|\bar{e}\|}=\frac{\bar{u}\cdot \bar{e}}{\|\bar{e}\|^2}\bar{e}$

Är du med?
Om det känns enklare kan du normera vektorn först och sedan strunta i att dela med något i projektionsformeln, eftersom den då redan har längden 1. Det är om du räknar med en onormerad riktningsvektor som du måste dela med normen i kvadrat.

D4NIEL skrev:

Du har med vektorn "två gånger". Därför kvadreras normen.

Det är bra om du väljer namn så att det framgår att vektorn är normerad. T.ex. kan du kalla den normerade vektorn $\hat{e}$ och den onormerade vektorn $\bar{e}$. Då är din formel

$\displaystyle \bar{u}^\prime=(\bar{u}\cdot \hat{e})\hat{e}=(\bar{u}\cdot \frac{\bar{e}}{\|\bar{e}\|})\frac{\bar{e}}{\|\bar{e}\|}=\frac{\bar{u}\cdot \bar{e}}{\|\bar{e}\|^2}\bar{e}$

Är du med?
Om det känns enklare kan du normera vektorn först och sedan strunta i att dela med något i projektionsformeln, eftersom den då redan har längden 1. Det är om du räknar med en onormerad riktningsvektor som du måste dela med normen i kvadrat.

Nu är jag till 100% med på hur man tar fram ekvationen och sambandet för en projektion på en linje. Men denna ekvationen har jag endast använt när man har två vektorer. Nu har vi en vektor t(1,1,1). Har svårt att koppla hur vi använder just den ekvationen för att lösa denna uppgiften. Var är vektorn u i detta fallet? 

Vektorn u är vektorn du ska projicera. Du har nu tagit fram en formel för att projicera en valfri vektor, vilken som helst, på linjen i uppgiften.

Nästa steg i lösningen är att i tur och ordning projicera basvektorerna i x-led, y-led och z-led och se var de hamnar. Varje basvektor ger motsvarande kolonn i avbildningsmatrisen $T$. Detta är ett "standardknep" som det står om i din bok!

Låt alltså i tur och ordning $u$ vara basvektorerna $(1,0,0)$, $(0,1,0)$ och $(0,0,1)$. Det som kanske krånglar till det lite för dig är att man ibland använder bokstaven e som beteckning även för basvektorer, t.ex. $\mathbf{e}_x,\mathbf{e}_y,\mathbf{e}_z$. För första kolonnen vill du alltså beräkna

$\displaystyle \bar{u}^\prime=(\mathbf{e}_x\cdot \bar{e})\bar{e}$

notera att det förmodligen blir lättare om man  döper om antingen basvektorerna eller riktningsvektorn för linjen, annars blir det många $e$

D4NIEL skrev:

Vektorn u är vektorn du ska projicera.

Nästa steg i lösningen är att i tur och ordning projicera basvektorerna i x-led, y-led och z-led och se var de hamnar. Varje basvektor ger motsvarande kolonn i avbildningsmatrisen $T$.

Låt alltså i tur och ordning $u$ vara basvektorerna $(1,0,0)$, $(0,1,0)$ och $(0,0,1)$. Det som kanske krånglar till det lite för dig är att man ibland använder bokstaven e som beteckning även för basvektorer, t.ex. $\mathbf{e}_x,\mathbf{e}_y,\mathbf{e}_z$. För första kolonnen vill du alltså beräkna

$\displaystyle \bar{u}^\prime=(\mathbf{e}_x\cdot \bar{e})\bar{e}$

notera att det förmodligen blir lättare om man  döper om antingen basvektorerna eller riktningsvektorn för linjen ,$\bar{e}$

Nu börjar jag känna igen mig. Jag blandar ihop projektion på linje och plan för metoderna vi lärt oss är rätt lika. Är skillnaden (i grova drag) att vi i planen har tre riktningsvektorer till basvektorerna medan vi har en riktningsvektor till basvektorerna och man därför inte kan skriva (x,y,z)=(x1,x2,x3)+t(1,1,1) för linjer? 

Tillägg: 24 aug 2023 16:32

Varför det inte funkar att projicera på samma sätt för linje i rummet är ju för att vi får oändligt många riktningar som är vinkelräta mot linjen och får ingen definitiv normalvektor.

Den stora skillnaden är att man vanligtvis använder normalen (som är vinkelrät mot planet) när man projicerar på ett plan,

$u^\prime=\bar{u}-(\bar{u}\cdot \hat{n})\hat{n}$

När man projicerar på en linje använder man en vektor som är parallell med linjen,

$u^\prime=(\bar{u}\cdot\hat{e})\hat{e}$

Ibland vill man spegla en vektor i ett plan, då blir det

$u^\prime=\bar{u}-2(\bar{u}\cdot \hat{n})\hat{n}$

Det är väldigt vanligt att man blandar ihop olika projektioner och speglingar. Men det brukar lösa sig om man är noga med att skissa en bild över situationen, antingen ett plan med en normal eller en linje med en riktningsvektor.

Du kan alltid uttrycka en linje som $(x,y,z)=(x_1,x_2,x_3)+t\bar{e}$

Men om man lägger linjen utanför origo dvs $(x_1,x_2,x_3)\neq (0,0,0)$ måste man vara vaksam. Var också noga med att förstå att en linje har oändlig utsträckning, olika värden på parametern $t$ ger olika punkter i den samlade punktmängden som utgör linjen. Försök skilja på punkter i rummet, vektorer och linjer.

D4NIEL skrev:

Den stora skillnaden är att man vanligtvis använder normalen (som är vinkelrät mot planet) när man projicerar på ett plan,

$u^\prime=\bar{u}-(\bar{u}\cdot \hat{n})\hat{n}$

När man projicerar på en linje använder man en vektor som är parallell med linjen,

$u^\prime=(\bar{u}\cdot\hat{e})\hat{e}$

Ibland vill man spegla en vektor i ett plan, då blir det

$u^\prime=\bar{u}-2(\bar{u}\cdot \hat{n})\hat{n}$

Det är väldigt vanligt att man blandar ihop olika projektioner och speglingar. Men det brukar lösa sig om man är noga med att skissa en bild över situationen, antingen ett plan med en normal eller en linje med en riktningsvektor.

Du kan alltid uttrycka en linje som $(x,y,z)=(x_1,x_2,x_3)+t\bar{e}$

Men om man lägger linjen utanför origo dvs $(x_1,x_2,x_3)\neq (0,0,0)$ måste man vara vaksam. Var också noga med att förstå att en linje har oändlig utsträckning, olika värden på parametern $t$ ger olika punkter i den samlade punktmängden som utgör linjen. Försök skilja på punkter i rummet, vektorer och linjer.

Tusen tusen tack för hjälpen!