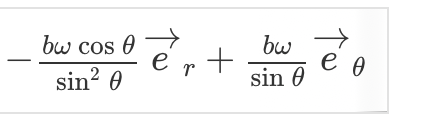Bestäm P:s hastighet och acceleration

Om $r\sin \theta =b$ så är väl $r=\frac{b}{\sin \theta }$.

Sedan är det givet att $\dot{\theta }=\omega =\mathrm{konstant}$.

PATENTERAMERA skrev:

Om $r\sin \theta =b$ så är väl $r=\frac{b}{\sin \theta }$.

Sedan är det givet att $\dot{\theta }=\omega =\mathrm{konstant}$.

Ja men vi har också en x-komponent för P:s koordinater. Varför försummar vi den när vi ska använda oss av cylinderkoordinater? Jag tänker mig att vi har r(theta)=(bcostheta/sintheta,b/sinheta,0)

Nja, i Kartesiska koordinater så har du att

$\overrightarrow{r}\left(r, \theta \right)=r\cos \theta {\overrightarrow{e}}_x+r\sin \theta {\overrightarrow{e}}_y$ = (med bivillkor $r\sin \theta =b$) = $r\cos \theta {\overrightarrow{e}}_x+b{\overrightarrow{e}}_y$.

PATENTERAMERA skrev:

Nja, i Kartesiska koordinater så har du att

$\overrightarrow{r}\left(r, \theta \right)=r\cos \theta {\overrightarrow{e}}_x+r\sin \theta {\overrightarrow{e}}_y$ = (med bivillkor $r\sin \theta =b$) = $r\cos \theta {\overrightarrow{e}}_x+b{\overrightarrow{e}}_y$.

Aa ok juste man kan se y=rsintheta=b då b anger höjden i det läge P befinner sig och x är då rcostheta.  Men då borde vi skriva r som funktion av theta som r(r,theta)=(rcostheta,b,0)

Ja, och om man löser ut r ur bivillkoret så har man

$\overrightarrow{r}=bcot\theta {\overrightarrow{e}}_x+b{\overrightarrow{e}}_y$. 

PATENTERAMERA skrev:

Ja, och om man löser ut r ur bivillkoret så har man

$\overrightarrow{r}=bcot\theta {\overrightarrow{e}}_x+b{\overrightarrow{e}}_y$. 

Yes ok nu kan man alltså derivera detta då ?

Ja.

PATENTERAMERA skrev:

Ja.

Problemet är att det blir inte rätt derivata för mig när jag deriverar bcostheta/sintheta map på tiden.

Gå inte över till polära basvektorer. Fortsätt med Kartesiska basvektorer ${\overrightarrow{e}}_x och {\overrightarrow{e}}_y$.

$\overrightarrow{v}=\dot{\overrightarrow{r}}=-\frac{b\omega }{{\sin }^2\theta }{\overrightarrow{e}}_x$.

PATENTERAMERA skrev:

Gå inte över till polära basvektorer. Fortsätt med Kartesiska basvektorer ${\overrightarrow{e}}_x och {\overrightarrow{e}}_y$.

$\overrightarrow{v}=\dot{\overrightarrow{r}}=-\frac{b\omega }{{\sin }^2\theta }{\overrightarrow{e}}_x$.

Men facit säger att det blir -bwcostheta/sin^2theta. Har de gjort fel?  Juste så man ska hålla sig till kartesiska basvektorer när man uttrycker r som funktion av theta?

Har facit uttryckt svaret i ${\overrightarrow{e}}_r och {\overrightarrow{e}}_{\theta }$ månne?

PATENTERAMERA skrev:

Har facit uttryckt svaret i ${\overrightarrow{e}}_r och {\overrightarrow{e}}_{\theta }$ månne?

Såhär ser det ut. Jag tror deras rprick är fel och deras v_theta förstår jag inte hur de har fått fram den 

Vi har att

$\overrightarrow{v}=-\frac{b\omega }{{\sin }^2\theta }{\overrightarrow{e}}_x=-\frac{b\omega }{{\sin }^2\theta }\left[\left({\overrightarrow{e}}_x·{\overrightarrow{e}}_r\right){\overrightarrow{e}}_r+\left({\overrightarrow{e}}_x·{\overrightarrow{e}}_{\theta }\right){\overrightarrow{e}}_{\theta }\right]=-\frac{b\omega }{{\sin }^2\theta }\left[\cos \theta {\overrightarrow{e}}_r-\sin \theta {\overrightarrow{e}}_{\theta }\right]=-\frac{b\omega \cos \theta }{{\sin }^2\theta }{\overrightarrow{e}}_r+\frac{b\omega }{\sin \theta }{\overrightarrow{e}}_{\theta }$.

Så samma som facit.

PATENTERAMERA skrev:

Vi har att

$\overrightarrow{v}=-\frac{b\omega }{{\sin }^2\theta }{\overrightarrow{e}}_x=-\frac{b\omega }{{\sin }^2\theta }\left[\left({\overrightarrow{e}}_x·{\overrightarrow{e}}_r\right){\overrightarrow{e}}_r+\left({\overrightarrow{e}}_x·{\overrightarrow{e}}_{\theta }\right){\overrightarrow{e}}_{\theta }\right]=-\frac{b\omega }{{\sin }^2\theta }\left[\cos \theta {\overrightarrow{e}}_r-\sin \theta {\overrightarrow{e}}_{\theta }\right]=-\frac{b\omega \cos \theta }{{\sin }^2\theta }{\overrightarrow{e}}_r+\frac{b\omega }{\sin \theta }{\overrightarrow{e}}_{\theta }$.

Så samma som facit.

Jag hänger tyvärr inte med nu. Vad är felet med att svara som -bw/sintheta?

Jag har bara uttryckt vektorn ${\overrightarrow{e}}_x$ i termer av ${\overrightarrow{e}}_r och {\overrightarrow{e}}_{\theta }$.

PATENTERAMERA skrev:

Jag har bara uttryckt vektorn ${\overrightarrow{e}}_x$ i termer av ${\overrightarrow{e}}_r och {\overrightarrow{e}}_{\theta }$.

Men varför ska man göra på det sättet? Det ser ut som en krånglig väg. Vi hade ju i början r(r,theta)=(bcostheta/sintheta)*ex+bey. Facit använde endast r=b/costheta som funktion , det ser enklare ut men jag undrar varför de nöjer sig med den funktionen bara?

För att visa att vårt svar är detsamma som facits svar.

Vi har svarat att v är

Facit har svarat att v är

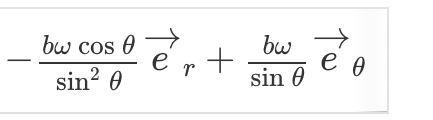
Det är bara två olika sätt att beskriva samma hastighetsvektor v.

Båda svaren är rätt.

PATENTERAMERA skrev:

För att visa att vårt svar är detsamma som facits svar.

Vi har svarat att v är

Facit har svarat att v är

Det är bara två olika sätt att beskriva samma hastighetsvektor v.

Båda svaren är rätt.

Ok jag förstår. Du använde definitionen av skalärprodukt mellan två vektorer för att få rätt på v och facit vill ha svaret i e_r och e_theta. Dock känns det som att man borde  ha allt uttryckt i e_r oche_theta från början för att slippa mellansteg

Det står inte explicit i uppgiften att man skall svara med just de basvektorerna. Känns naturligare att använda e_x i detta problem eftersom hastighet och acceleration uppenbart är parallella med x-axeln.

PATENTERAMERA skrev:

Det står inte explicit i uppgiften att man skall svara med just de basvektorerna. Känns naturligare att använda e_x i detta problem eftersom hastighet och acceleration uppenbart är parallella med x-axeln.

Nej ok. Jag håller med. Jag ser nu i facit att de inte uttrycket ens v_r med e_r och v_theta med e_theta. De verkar ha slarvat bort det.

Jag förstår inte vad som har hänt med rthetaprick i uttrycket för hastigheten i cylinderkoordinater

De har bara deriverat uttrycket för r i ekvation (1).

$\frac{dr}{dt}=\frac{d}{dt}\left(\frac{b}{\sin \theta }\right)=-\frac{b\omega \cos \theta }{{\sin }^2\theta }$.

Vad det det du undrade över?

PATENTERAMERA skrev:

De har bara deriverat uttrycket för r i ekvation (1).

$\frac{dr}{dt}=\frac{d}{dt}\left(\frac{b}{\sin \theta }\right)=-\frac{b\omega \cos \theta }{{\sin }^2\theta }$.

Vad det det du undrade över?

Ja men det är lite förvirrande för jag och facit har gjort olika. Jag hade r(r,theta)=bcostheta/sinthetaex+bey. Cylinderkoordinater för hastigheten ges ju som rpricke_r +rthetapricke_theta

Hur beräknade du dr/dt?

Du måste skilja på $\overrightarrow{r}$ (en vektor) och $r=\left|\overrightarrow{r}\right|$ (en skalär).

PATENTERAMERA skrev:

Du måste skilja på $\overrightarrow{r}$ (en vektor) och $r=\left|\overrightarrow{r}\right|$ (en skalär).

Jag tror inte du förstår mig nu. Se bild nedan. Som du ser har jag bara räknat rprick , men vi har en term till som heter rtheta i v för cylinderkoordinater. Vilken r ska jag stoppa in här?

Den första ekvationen är en vektorekvation. Är det det som du undrade över.

PATENTERAMERA skrev:

Den första ekvationen är en vektorekvation. Är det det som du undrade över.

Nej det är inte det jag undrade över. Kolla på steg 2. Jag är inte klar för jag saknar rthetaprick, den där r vet jag inte vilken r det menas med. 

Vad menar du med steg 2?

PATENTERAMERA skrev:

Vad menar du med steg 2.

"Betrakta  hastigheten i cylinderkoordinater".

Ja, det är ju en känd formel för hastigheten i polära- eller cylinderkoordinater. Det härleds säkert någonstans i boken. Var det det du undrade över?

PATENTERAMERA skrev:

Ja, det är ju en känd formel för hastigheten i polära- eller cylinderkoordinater. Det härleds säkert någonstans i boken. Var det det du undrade över?

Nej det är inte det jag undrade över. Justnu har jag -bw/sin^2theta+rw=v men facit har bara vx=-bw/sin^2theta  så min fråga är vad hände med rw termen i cylinderkoordinater för v. Vilken r används i den formeln för v i cylinderkoordinater?

Vi har att r = $\frac{b}{\sin \theta }$. Då får vi att $\dot{r}=\frac{d}{dt}\left(\frac{b}{\sin \theta }\right)=\frac{d}{d\theta }\left(\frac{b}{\sin \theta }\right)\frac{d\theta }{dt}=-\frac{b\omega \cos \theta }{{\sin }^2\theta }$.

Sätt in detta i formeln $\overrightarrow{v}=\dot{r}{\overrightarrow{e}}_r+r\omega {\overrightarrow{e}}_{\theta }$.

PATENTERAMERA skrev:

Vi har att r = $\frac{b}{\sin \theta }$. Då får vi att $\dot{r}=\frac{d}{dt}\left(\frac{b}{\sin \theta }\right)=\frac{d}{d\theta }\left(\frac{b}{\sin \theta }\right)\frac{d\theta }{dt}=-\frac{b\omega \cos \theta }{{\sin }^2\theta }$.

Sätt in detta i formeln $\overrightarrow{v}=\dot{r}{\overrightarrow{e}}_r+r\omega {\overrightarrow{e}}_{\theta }$.

Fast du använder facits ekvation (1) och den vill jag inte använda för det var inte så vi började. Hela min fråga handlar om vår vektor r(r,theta) i kartesiska koordinater som vi började med.. Sen om du menar vår metod är fel men facits metod är rätt så får du gärna förklara varför ekvation (1) formulerades i facit. Justnu vill jag förstå vår metod som vi använde för att vi ska få samma svar som facit. Vi har rprick som -bw/sin^2theta men saknar rthetaprick i vår metod. 

(1) följer ju direkt från figuren och enkel trigg.

Annars så har vi att

$\overrightarrow{r}=bcot\theta {\overrightarrow{e}}_x+b{\overrightarrow{e}}_y, r = \left|\overrightarrow{r}\right| = \sqrt{b^2\left(co{t}^2\theta + 1\right)}=\frac{b}{\sin \theta }$.

PATENTERAMERA skrev:

(1) följer ju direkt från figuren och enkel trigg.

Annars så har vi att

$\overrightarrow{r}=bcot\theta {\overrightarrow{e}}_x+b{\overrightarrow{e}}_y, r = \left|\overrightarrow{r}\right| = \sqrt{b^2\left(co{t}^2\theta + 1\right)}=\frac{b}{\sin \theta }$.

Ok detta förstår jag. r är alltså beloppet av vår r(r,theta). Men då har vi detta nedan se bild. Är det rätt då?

Inte riktigt. Se #35 för beräkning av r-prick.

PATENTERAMERA skrev:

Inte riktigt. Se #35 för beräkning av r-prick.

Jag blir nu på riktigt förvirrad. Jag använde mig av vektorn r(r, theta) för att derivera r.

Visa.

Tillägg: 21 feb 2026 18:56

Det är skillnad på $\dot{r} och \dot{\overrightarrow{r}}$.

PATENTERAMERA skrev:

Visa.

---

Tillägg: 21 feb 2026 18:56

Det är skillnad på $\dot{r} och \dot{\overrightarrow{r}}$.

Såhär fick jag. 

Du har beräknat $\dot{\overrightarrow{r}}$ och inte $\dot{r}$. Du får inte blanda ihop vektorer och skalärer.

PATENTERAMERA skrev:

Du har beräknat $\dot{\overrightarrow{r}}$ och inte $\dot{r}$. Du får inte blanda ihop vektorer och skalärer.

Så derivatan av en vektor är det jag beräknade medan derivatan av en skalär map tiden är det formeln syftar på när det gäller v och a i cylinderkoordinater? Om jag förstår dig rätt så har vi tagit fram en vektorfunktion för r men vi deriverar beloppet av den där r map tiden?

Ja, $\overrightarrow{r}$ är ortsvektorn, och r är ortsvektorns belopp/längd.

PATENTERAMERA skrev:

Ja, $\overrightarrow{r}$ är ortsvektorn, och r är ortsvektorns belopp/längd.

Så rprick (utan vektorstreck) är derivatan av längden r dvs hur snabbt avståndet från origo förändras. 

Ja, precis.

PATENTERAMERA skrev:

Ja, precis.

Men hur får man vx då? Det verkar tydligen inte räcka med att bestämma endast dessa två komponenter av v.

v_x = $\overrightarrow{v}·{\overrightarrow{e}}_x$

Utnyttja att ${\overrightarrow{e}}_x·{\overrightarrow{e}}_r=\cos \theta , {\overrightarrow{e}}_x·{\overrightarrow{e}}_{\theta }=-\sin \theta$.

PATENTERAMERA skrev:

v_x = $\overrightarrow{v}·{\overrightarrow{e}}_x$

Utnyttja att ${\overrightarrow{e}}_x·{\overrightarrow{e}}_r=\cos \theta , {\overrightarrow{e}}_x·{\overrightarrow{e}}_{\theta }=-\sin \theta$.

Varför är vi så intresserad av att få fram vx här och inte generella hastighetsvektorn i cylinderkoordinater som jag skrivit i #48?

Vet inte. Man har ju bara frågat om hastighet och acceleration utan att specificera vilka basvektorer som skall användas.

PATENTERAMERA skrev:

Vet inte. Man har ju bara frågat om hastighet och acceleration utan att specificera vilka basvektorer som skall användas.

Ok,jag misstänker att man vill få fram vx och ax då P rör sig enbart i x-riktning och inte i y-led.

Ja, fast då känns det lite som att gå över ån efter vatten att blanda in ${\overrightarrow{e}}_r och {\overrightarrow{e}}_{\theta }$.

PATENTERAMERA skrev:

Ja, fast då känns det lite som att gå över ån efter vatten att blanda in ${\overrightarrow{e}}_r och {\overrightarrow{e}}_{\theta }$.

Det är därför jag stör mig på facits svar på P:s haastighet och acceleration. De kan inte säga till oss om de är ute efter x komponenten eller y komponenten av v eller den generella hastigheten i cylinderkoordinater. Det makear inte sense att bara räkna ut vx och ax utan någon skäl. De har dock blandat in e_r och e_theta för att få fram vx.