Bestäm reaktionskrafterna RA och RO på axeln

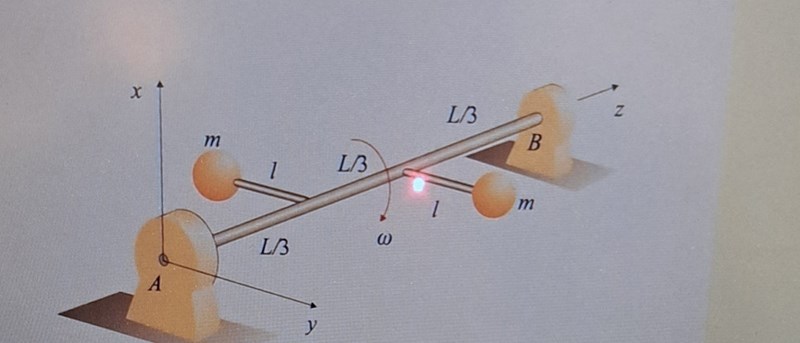
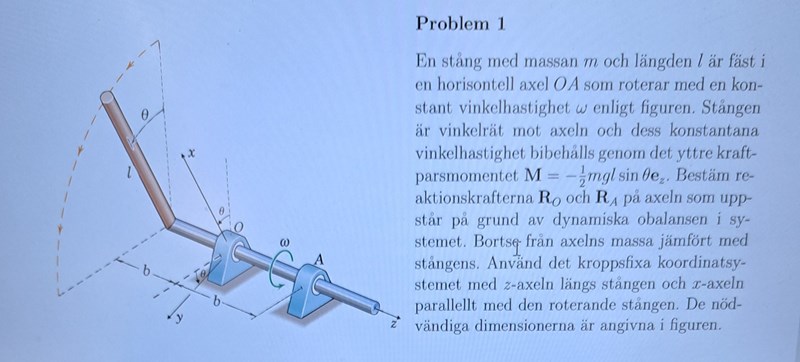
I det problemet ligger G fixt (samma ställe hela tiden) ingen hastighet, ingen acceleration. I ditt problem så rör sig G i en cirkelbana och accelererar därför.

PATENTERAMERA skrev:

I det problemet ligger G fixt (samma ställe hela tiden) ingen hastighet, ingen acceleration. I ditt problem så rör sig G i en cirkelbana och accelererar därför.

Jag förstår inte varför det sker ingen acceleration och hastighet då G ligger på samma ställe i första bildproblemet? Sen undrar jag hur man vet att G rör sig i en cirkelbana och har därför en acceleration? Har detta att göra med att G: s koordinater i andra bildproblemet inte är 0 som i första bildproblemet där G endast har (0,0,0)?

Om någonting är stilla så har det varken hastighet eller acceleration. Eller hur?

Om en stel kropp roterar kring en axel så rör sig masscentrum alltid i en cirkelbana runt axeln, om inte masscentrum ligger på axeln förstås (som i det första problemet). Rita en figur och fundera lite så klarnar det nog.

PATENTERAMERA skrev:

Om någonting är stilla så har det varken hastighet eller acceleration. Eller hur?

Om en stel kropp roterar kring en axel så rör sig masscentrum alltid i en cirkelbana runt axeln, om inte masscentrum ligger på axeln förstås (som i det första problemet). Rita en figur och fundera lite så klarnar det nog.

jag hänger tyvärr inte med och därför kan inte jag skissa en figur. Jag är med på att om något är stilla så har den varken hastighet eller acceleration, men jag förstår inte om du menar att stången är stilla eller om dessa masscentrum är stilla som i första problemet där stången roterar kring z-axeln dvs sin egen axel som den ligger på ? men är inte stången stilla även i det andra problemet trots att w roterar i z-axeln som är OA-axeln?

Stången roterar men G ligger i detta fall på z-axeln (rotationsaxeln) och ligger därför still.

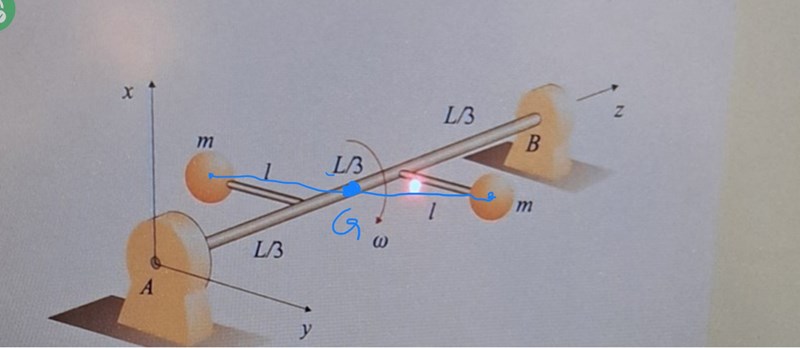
PATENTERAMERA skrev:

Stången roterar men G ligger i detta fall på z-axeln (rotationsaxeln) och ligger därför still.

Okej så om G ligger på rotationsaxeln så är den stilla och roterar ej även om stången självt roterar kring sin egen axel (första bildproblemet)? Men i vårt andra problem så roterar stången och då är G inte konstant för den ligger inte på rotationsaxeln utan roterar kring den som stången gör ?

Precis.

PATENTERAMERA skrev:

Precis.

Ok. Du sa att masscentrum alltid rör sig i en cirkelbana runt axeln , är det även så för stången om detta alltid gäller för masscentrum ? Min andra fråga är om vi ska använda oss av accelerationssambandet för att hitta a_G = a_O+wx(wxr_OG) till problem 1? 

Det är formeln för hastigheter.

För acceleration så gäller

${\overrightarrow{a}}_C={\overrightarrow{a}}_O+\overrightarrow{\alpha }\times {\overrightarrow{r}}_{OC}+\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times {\overrightarrow{r}}_{OC}\right)$.

OK, du ändrade då är det rätt.

PATENTERAMERA skrev:

Det är formeln för hastigheter.

För acceleration så gäller

${\overrightarrow{a}}_C={\overrightarrow{a}}_O+\overrightarrow{\alpha }\times {\overrightarrow{r}}_{OC}+\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times {\overrightarrow{r}}_{OC}\right)$.

OK, du ändrade då är det rätt.

Ja precis. Jag ändrade det. kan du svara på min första fråga i #9?

Ja det gäller för godtycklig stel kropp, så länge som masscentrum inte ligger på själva rotationsaxeln.

PATENTERAMERA skrev:

Ja det gäller för godtycklig stel kropp, så länge som masscentrum inte ligger på själva rotationsaxeln.

Ok. Då förstår jag.

Det är så att jag försökte använda mig tidigare av denna summa för att få fram komponenterna  men misslyckades med I_yy samt I_zz. Jag tänkte att stångens längd är l och den har en komponent som är -b i z -led, alltså får vi m(l^2+b^2) och för I_zz blir det ml^2 då y =0. Varför stämmer inte dessa värden på tröghetskomponenterna? Utgår man från stångens G till O när man använder dessa tröghetsummor ? Målet var ju att skapa I_O matrisen i problem 1.

Bump

Kan man göra som jag tänkte med summorna i bilden från #14?

Du kan använda steiners sats. Tex

I_xx = (I_G)_xx + m((y_G)² + (z_G)²) = 0 + mb² = mb².

PATENTERAMERA skrev:

Du kan använda steiners sats. Tex

I_xx = (I_G)_xx + m((y_G)² + (z_G)²) = 0 + mb² = mb².

Ja precis. Men är det samma sak som att använda de här summorna då? Sen förstår jag inte varför I_gxx=0 ? I_gxx för en homogen stång är väl ml²/12 . Jag tänkte mig I_Oxx=I_Gxx+m(y_G²+z_G²)

Jag antar att det är en smal stång så att vi kan försumma I_Gxx. Eftersom man inte fått någon information om stångens tjocklek så är det säkert tänkt att man skall göra den approximationen. Obs ml²/12 är för en axel genom masscentrum vinkelrät mot stången. x-axeln är parallell med stången.

PATENTERAMERA skrev:

Jag antar att det är en smal stång så att vi kan försumma I_Gxx. Eftersom man inte fått någon information om stångens tjocklek så är det säkert tänkt att man skall göra den approximationen. Obs ml²/12 är för en axel genom masscentrum vinkelrät mot stången. x-axeln är parallell med stången.

Jaha ok så om x-axeln inte är vinkelrät mot stångens masscentrum så kan vi inte säga att Igxx=1/12ml²? Isåfall har vi ingen kännedom om Igxx och då kan man säga att den är 0 då x-axeln är parallell med stången och går inte ens igenom den så att den blir vinkelrät.

Eftersom stången är smal så blir I_Gxx litet, jämfört med I_Gyy och I_Gzz, så det är tänkt att man kan försumma I_Gxx och se den som i princip 0. Annars får man ta med I_Gxx som en ytterligare obekant, men det tror jag inte man tänkt sig.

PATENTERAMERA skrev:

Eftersom stången är smal så blir I_Gxx litet, jämfört med I_Gyy och I_Gzz, så det är tänkt att man kan försumma I_Gxx och se den som i princip 0. Annars får man ta med I_Gxx som en ytterligare obekant, men det tror jag inte man tänkt sig.

Ok. Men du nämnde innan att för en axel genom masscentrum vinkelrät mot stången för Igxx så är det ml^2/12 för en smal stång. Men hur är det om man vill utnyttja parallellförflyttningssatsen för att få fram I_Oyy =Ig_yy+m(x_g²+z_g²)? y-axeln är väl inte vinkelrät mot stången som z-axeln? Det vinkelräta avståndet från G till O , blir det då i detta fall d= l²/4+b²?

Jo, du får parallellförskjuta y-axeln så att den går genom G. Då är den vinkelrät mot stången. Så I_Gyy = ml²/12

PATENTERAMERA skrev:

Jo, du får parallellförskjuta y-axeln så att den går genom G. Då är den vinkelrät mot stången. Så I_Gyy = ml²/12

Ok. Så I_Oyy=ml²/48+ml²/4+mb²?

Var kom 48 ifrån?

PATENTERAMERA skrev:

Var kom 48 ifrån?

Stångens masscentrum har ju l/2 och inte l. För Igyy=ml^2/12 så antar jag att man menar masscentrums längd eller? Eller nej det är ju stångens längd. Hur blir det med I_gzz som är 1/12m(a²+b²)? En sista fråga dock är de här summorna som anger Ixx ,Iyy  osv i #13. Är det som att använda steiners sats eller? För det verkar inte passa att använda för att ta reda på varje komponeterna för I_o efrersom vi måste flytta från G till O. 

Tillägg: 10 okt 2025 17:04

Lyckades lösa detta mha steiners på I_ozz.